CONSTANT FUNCTION: Let k be a fixed real number. Then a function f (x) given by f (x) = k for all x ϵ R is called a constant function. Sometimes we also call it the constant function k.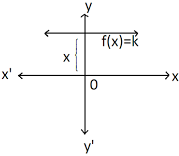
IDENTITY FUNCTION: The function defined by I (x) = x for all x ϵ R is called the identity function on R.
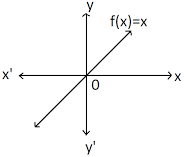RECIPROCAL FUNCTION: The function that associates each non-zero real number x to its reciprocal 1/x is called the reciprocal function.
The domain and range of the reciprocal function are both equal to R – {0} i.e., the set of all non-zero real numbers.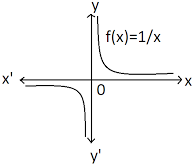
SQUARE ROOT FUNCTION: The function that associates every positive real number x to +√x is called the square root function i.e. f(x) = +√x.
Negative real numbers do not have real square roots. So, f (x) is not defined when is a negative real number. Therefore, domain of f is the set of all non-negative real numbers = [0, ∞).
Range (f) = {+√x | x ϵ [0, ∞)} = [0, ∞).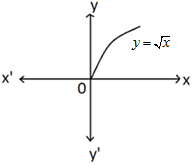
LOGARITHMIC FUNCTION: If ‘a’ is a positive real number, then the function that associates every positive real number to loga x i.e., f (x) = loga x is called the logarithmic function.
The domain of the logarithmic function is the set of all positive real numbers and the range is the set R of all real numbers.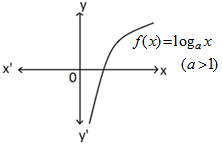
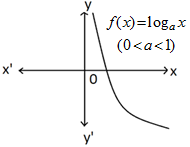EXPONENTIAL FUNCTION: If a is positive real number, then the function which associates every real number x to ax i.e., f (x) = ax is called the exponential function.
The domain of the exponential function is R and the range is the set of all positive real numbers.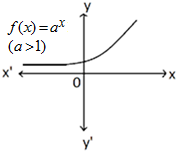
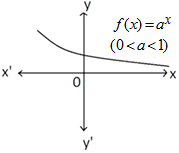SQUARE FUNCTION: A function given by f(x) = x2 is called the square function.
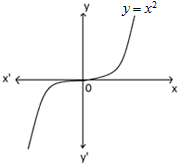
The domain of the square function is R and its range is [0, ∞). The equation of the curve represented by the square function is y= x2.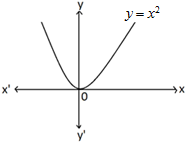 
CUBE FUNCTION: A function given by f(x) = x3 is called the cube function.
The domain and range of cube function are both equal to R.