General Equation of Conic
If focus, directrix and eccentricity of conic are given, then
- Let S (α, β) be focus, ax + by + c = 0 be directrix. Let e be the eccentricity of conic.
- Let P (h, k) be any point on the conic such that PM is perpendicular from P on the directrix.
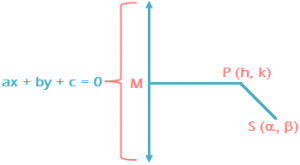
SP = e SM
SP² = e² SM²
(h – α)² + (k – β)² = e²\(\left\{ \frac{ah+bk+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right\}\)
Locus of (h, k) is (x – α)² + (y – β)² = e²\(\left\{ \frac{ax+by+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right\}\)
This is the equation of required conic.
This equation when simplified can be written in form ax² + 2hxy + by² + 2gx + 2fy + c = 0
That is ax² + 2hxy + by² + 2gx + 2fy + c = 0
A pair of straight line, if Δ = abc + 2fgh – af² – bg² – ch²
A pair of parallel straight lines, if Δ = 0 and h² = ab
A pair of perpendicular lines. If Δ = 0 and a + b = 0
A point if Δ = 0 and h² < ab
If represent circle if Δ ≠ 0, a = b and h = 0
- A parabola, if Δ ≠ 0 and h² = ab
- An ellipse, if Δ ≠ 0 and h² < ab
- A hyperbola, if Δ ≠ 0 and h² > ab
- Rectangular hyperbola, if Δ ≠ 0 and h² > ab and a + b = 0.
Some useful terms in conics
- Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of conic section.
- Vertex: The points of intersection of the conic section and the axis are called the vertex of conic section
- Centre: The point which bisects every chord of conic passing through it, is called centre of the conic section.
- Latus rectum: The latus rectum of conic is the chord passing through focus and perpendicular to axis.
- Focal chord: Any chord passing though the focus is called focal chord of a conic.
- Double ordinate: A chord perpendicular to the axis of a conic is known as double ordinate.
Latus rectum is a double – ordinate passing through the focus of parabola. If ax² + 2hxy + by² + 2gx + 2fy + c = 0
Is the equation of conic, then the co – ordinates of its centre are \(\left( \frac{hf-bg}{ab-{{h}^{2}}},\frac{hg-af}{ab-{{h}^{2}}} \right)\).
If focus, directrix and eccentricity of conic are given, then
- Let S (α, β) be focus, ax + by + c = 0 be directrix. Let e be the eccentricity of conic.
- Let P (h, k) be any point on the conic such that PM is perpendicular from P on the directrix.
SP = e SM
SP² = e² SM²
(h – α)² + (k – β)² = e²\(\left\{ \frac{ah+bk+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right\}\)
Locus of (h, k) is (x – α)² + (y – β)² = e²\(\left\{ \frac{ax+by+c}{\sqrt{{{a}^{2}}+{{b}^{2}}}} \right\}\)
This is the equation of required conic.
This equation when simplified can be written in form ax² + 2hxy + by² + 2gx + 2fy + c = 0
That is ax² + 2hxy + by² + 2gx + 2fy + c = 0
A pair of straight line, if Δ = abc + 2fgh – af² – bg² – ch²
A pair of parallel straight lines, if Δ = 0 and h² = ab
A pair of perpendicular lines. If Δ = 0 and a + b = 0
A point if Δ = 0 and h² < ab
If represent circle if Δ ≠ 0, a = b and h = 0
- A parabola, if Δ ≠ 0 and h² = ab
- An ellipse, if Δ ≠ 0 and h² < ab
- A hyperbola, if Δ ≠ 0 and h² > ab
- Rectangular hyperbola, if Δ ≠ 0 and h² > ab and a + b = 0.
Some useful terms in conics
- Axis: The straight line passing through the focus and perpendicular to the directrix is called the axis of conic section.
- Vertex: The points of intersection of the conic section and the axis are called the vertex of conic section
- Centre: The point which bisects every chord of conic passing through it, is called centre of the conic section.
- Latus rectum: The latus rectum of conic is the chord passing through focus and perpendicular to axis.
- Focal chord: Any chord passing though the focus is called focal chord of a conic.
- Double ordinate: A chord perpendicular to the axis of a conic is known as double ordinate.
Latus rectum is a double – ordinate passing through the focus of parabola. If ax² + 2hxy + by² + 2gx + 2fy + c = 0
Is the equation of conic, then the co – ordinates of its centre are \(\left( \frac{hf-bg}{ab-{{h}^{2}}},\frac{hg-af}{ab-{{h}^{2}}} \right)\).
