Gay – Lussac’s Law (or) Pressure Law
Gay – Lussac’s law is the relationship between the pressure and the temperature of a gas. According to the law, when volume is held constant, the pressure of an ideal gas is directly proportional to its temperature. At a given volume, the pressure of a given mass of gas is proportional to its absolute temperature. It is also known as Charle’s Law for Pressure.
In fact, this is the definition of the absolute temperature T. If one starts from the fact that v²rms α T and uses the fact that V is constant, one gets from kinetic theory of gases.
P α v²rms (Or) P α T
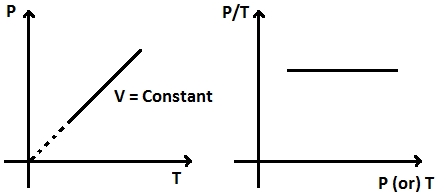
The volume remaining constant, the pressure of a given mass of a gas is directly proportional to its absolute temperature.
P/ T = Constant
∴ \(\frac{{{P}_{1}}}{{{T}_{1}}}\,\,=\,\,\frac{{{P}_{2}}}{{{T}_{2}}}\).
Thus, P – T graph is a straight line passing through origin or P/T versus P or T graph is a straight line parallel to P or T axis.
How to find the Gay – Lussac’s Law (or) Pressure Law?
Problem: At temperature 250K, a gas in a cylinder has a pressure of 1.5 atm. If the initial pressure of the gas was 1 atm. What was its initial temperature?
Solution: Given,
Initial Pressure (P₁) = 1 atm
Final Pressure (P₂) = 1.5 atm
Final temperature (T₂) = 250 K
Initial temperature (T₁) =?
Using Gay – Lussac’s Law (Or) Pressure Law:
\(\frac{{{P}_{1}}}{{{T}_{1}}}\,\,=\,\,\frac{{{P}_{2}}}{{{T}_{2}}}\),
\({{T}_{1}}\,\,=\,\,\frac{{{P}_{1}}{{T}_{2}}}{{{P}_{2}}}\,\,=\,\,\frac{(1\,atm\times 250\,K)}{1.5\,atm}=166.67K\).
Therefore,
Initial temperature (T₁) – 166.67 K.
