Forces between Multiple Charges
Charge is an inherent property of every atom, an atom is said to be charged if it has irregular number of electrons and protons, an atom is said to be positively charged if it has less number of electrons than protons, and negatively charged if it has more number of electrons than protons.
Bodies get charged in different way, the most common way of charging a body is to rub, if you rub a plastic comb with your hair, the comb attains electrons from our hair, now if we get tiny pieces of paper close to the comb the comb attracts the pieces like a magnet attracting iron fillings, this is because the electrons attract the positive charge on the paper. This is the force of charges in action.
How to calculate the magnitude of force between two charges?
We can find the force between any two charges by coulomb’s law, coulomb’s law states that two charged bodies will attract or repel each other with a force that proportional to the product of their masses and inversely proportional to the square of the distance between them,
Let’s get an equation out of this,
\(F\,=\,k\frac{{{Q}_{1}}\times {{Q}_{2}}}{{{d}^{2}}}\).
Where,
F = Force of attraction of repulsion depending upon the charges
K = Coulombs constant, for air it is 9 × 10⁹ N.m²/C²
Q₁ and Q₂ are the magnitudes of two charges
d = Distance between the two charges.
This is only applicable for two charged particles, how will we find a force on one charge due to multiple charges?
Let’s consider 3 charges QA, QB and QC.
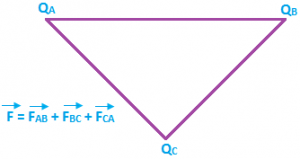
We could get the net force acting on a charge by calculating the vector some of all the forces acting on the charge, this is called the superposition theorem.
Considering the above example of 3 point charges QA, QB and QC with a position vector of r₁, r₂ and r₃. Then the force experienced by one charge due to the other charges is given by \(\overrightarrow{F}\,=\,\overrightarrow{{{F}_{AB}}}\,+\,\overrightarrow{{{F}_{BC}}}\,+\,\overrightarrow{{{F}_{CA}}}\).
This can be written as \(\overrightarrow{{{F}_{1}}}\,=\,\sum\nolimits_{j=1}^{n}{{{F}_{ij}}}\) (Where j ≠ i).
By applying this to our current situation of 3 point charges we will get \(\overrightarrow{{{F}_{1}}}\,=\,\frac{1}{4\pi {{\varepsilon }_{0}}}\left[ \frac{{{Q}_{A}}{{Q}_{B}}}{{{r}^{2}}_{AB}}\,{{\widehat{r}}_{AB}}\,+\,\frac{{{Q}_{A}}{{Q}_{C}}}{{{r}^{2}}_{AC}}{{\widehat{r}}_{AC}} \right]\).
This is a combination of the coulombs law and the superposition theorem, and any electro static force can be derived using coulombs law and the superposition theorem this way.
- The force acting on a charge is directly proportional to the magnitude of the charge, and inversely proportional to the square of the distance between them.
- The force acting on a point charge due to multiple charges is given by the vector sum of all individual forces acting on the charges.
