Floatation

(1) Translatory equilibrium: When a body of density ρ and volume V is immersed in a liquid of density σ, the forces acting on the body are

Weight of body W = mg = Vρg, acting vertically downwards through centre of gravity of the body.

Up thrust force = Vσg acting vertically upwards through the centre of gravity of the displaced liquid i.e., center of buoyancy.

If density of body is greater than that of liquid ρ > σ Weight will be more than up thrust so the body will sink.

If density of body is equal to that of liquid ρ = σ Weight will be equal to up thrust so the body will float fully submerged in neutral equilibrium anywhere in the liquid.

If density of body is lesser than that of liquid ρ < σ Weight will be less than up thrust so the body will move upwards and in equilibrium will float partially immersed in the liquid Such that, W = Vin σ g => v ρ g = Vin σ g, V ρ = Vin σ Where Vin is the volume of body in the liquid.

Important Points:

(i) A body will float in liquid only and only if ρ ≤ σ

(ii) In case of floating as weight of body = up thrust

So W_App = Actual weight – up thrust = 0

(iii) In case of floating Vρg = V_in σ g

So the equilibrium of floating bodies is unaffected by variations in g though both thrust and weight depend on g.

(2) Rotatory Equilibrium: When a floating body is slightly tilted from equilibrium position, the centre of buoyancy B shifts. The vertical line passing through the new centre of buoyancy B¢ and initial vertical line meet at a point M called meta-centre. If the meta-centre M is above the centre of gravity the couple due to forces at G (weight of body W) and at  (up thrust) tends to bring the body back to its original position. So for rotational equilibrium of floating body the meta-centre must always be higher than the centre of gravity of the body.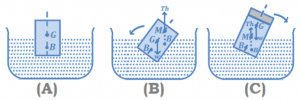However, if meta-center goes below CG, the couple due to forces at G and  tends to topple the floating body.

That is why a wooden log cannot be made to float vertical in water or a boat is likely to capsize if the sitting passengers stand on it. In these situations CG becomes higher than MC and so the body will topple if slightly tilted.

(3) Application of floatation:

(i) When a body floats then the weight of body = Up thrust

Vρg = V_in σ g Þ V_in = (ρ/ σ) V

∴ V_out = V – V_in = (1 – [ρ/ σ]) V

i.e., Fraction of volume outside the liquid f_out = V_out/ V = (1 – [ρ/ σ])

(ii) For floatation V ρ = V_in σ Þ  ρ = [V_in/ V] σ = f_in σ

If two different bodies A and B are floating in the same liquid then ρ_A/ ρ_B = (f_in)_A / (f_in)_B

(iii) If the same body is made to float in different liquids of densities σ_A and σ_B respectively.

V ρ = (V_in)_A σ_A = (V_in)_B σ_B

∴ σ_A/ σ_B = (V_in)_B/ (V_in)_A

(iv) If a platform of mass M and cross-section A is floating in a liquid of density σ with its height h inside the liquid

Mg = hA σg     …… (i)

Now if a body of mass m is placed on it and the platform sinks by y then

(M + m)g = (y + h)A σg                       …… (ii)

Subtracting equation (i) and (ii),

mg = Aσyg, i.e., W α y                        …… (iii)

So we can determine the weight of a body by placing it on a floating platform and noting the depression of the platform in the liquid by it.