Expression for Gravitational Potential at a Point
Gravitational potential at a point in a gravitational field of a body is defined as the amount of work done in bringing a body of unit mass from infinity to that point without acceleration.
Let, earth to be a perfect sphere of radius R and mass M. The mass of the earth can be supposed to be concentrated at its centre O and now let us calculate the gravitational potential at any point P, where OP = r and r > R. Join OP and produce it onwards. Take two-point A and B on this line such that OA = x and AB = dx.
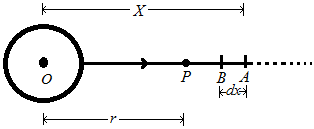
The gravitational force of attraction on a body of unit mass at point A will be:
\(F=\frac{GM\times 1}{{{x}^{2}}}=\frac{GM}{{{x}^{2}}}\).
Small amount of work done in bringing the unit mass of the body without acceleration through a small distance AB is:
\(dW=Fdx=\frac{GM}{{{x}^{2}}}dx\).
Total work done in bringing the body of unit mass from infinity to point P ca be obtained by integrating the above expression within the limits x = ∞ to x = r, we get:
∴ \(W=\int\limits_{\infty }^{r}{\frac{GM}{{{x}^{2}}}}dx=-\left( \frac{GM}{x} \right)_{\infty }^{r}=-GM\left[ \frac{1}{r}-\frac{1}{\infty } \right]=-\frac{GM}{r}\).
This work done is the measure of gravitational potential at P (i.e. VP)
\({{V}_{P}}=W=-\frac{GM}{r}\)… (1)
From equation (1):
1. The gravitational potential at a point is always negative.
2. When r = ∞ from (1), VP = 0 hence gravitational potential is maximum at infinity.
3. At the surface of earth, r = R therefore \({{V}_{P}}=-\frac{GM}{R}\) at the surface of earth.
The unit of gravitational potential is J/ kg. Dimensional formula of gravitational potential is:
\(\frac{Work}{Mass}=\frac{\left[ M{{L}^{2}}{{T}^{-2}} \right]}{\left[ M \right]}=\left[ {{M}^{0}}{{L}^{2}}{{T}^{-2}} \right]\).
Gravitational potential is a scalar field because at any point in space it has only magnitude and no direction.
