Equation of Continuity
The continuity equation describes the transport of some quantities like fluid or gas. The equation explains how a fluid conserves mass in its motion. Many physical phenomena like energy, mass, momentum, natural quantities and electric charge are conserved using the continuity equations. This equation provides very useful information about the flow of fluids and its behaviour during its flow in a pipe or hose. The hose, a flexible tube, whose diameter decreases along its length has a direct consequence. The volume water flowing through the hose must be equal to the flow rate on the other end. The flow rate formula.
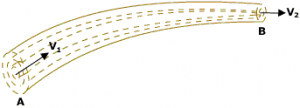
Consider a non-viscous liquid in streamline flow through a tube AB, of varying cross-section. Let A1 and A2 be the area of cross-section at A and B respectively.
The volume of water entering A per second = A₁V₁
Volume = Area x distance
\(\frac{Volume}{time}\,\,\,=\,\,\,Area\,\,\,\times \,\,\,\frac{dis\tan ce}{time}\)
= Area x Velocity
Where,
V₁ = Velocity of the flow of liquid at A
The volume of water leaving B per second = A₂v₂
∴ Mass of liquid entering per second at A = A₁v₁ρ₁
Mass of liquid leaving per second at B = A₂v₂ρ₂
Assuming there is no loss of liquid in tube and for free steady flow,
Mass of liquid entering per second at A = Mass of liquid leaving per second at B
i.e A₁v₁ρ₁ = A₂v₂ρ₂
Since the density is uniform throughout, ρ₁ = ρ₂
∴ A₁v₁ = A₂v₂
(Or)
Av = Constant
This is the equation of continuity.
Fluid Dynamics: The continuity equation in fluid dynamics describes that in any steady state process, the rate at which mass leaves the system is equal to the rate at which mass enters a system. The differential form of the continuity equation is:
\(\frac{\partial \rho }{\partial t}\,+\,\nabla .\,(\rho \,u)=\,0\)
Where,
t = time
ρ = Fluid density
u = Fluid velocity vector field.
How to find the Equation of Continuity?
Problem: Water travels through a hose at 0.8 meters per second. If the cross-sectional area of the exit nozzle is one-fifth that of the hose, at what speed does water exit the hose?
Solution: Given,
A₂ = ⅕ A₁
v₁ = 0.80 m/sec
Using Continuity Equation:
A₁v₁ = A₂v₂
A₁v₁ = ⅕ A₂v₂
v₂ = 5 v₁
v₂ = 5 x 0.80 m/sec
v₂ = 4 m/sec.
