Equation of a Plane Progressive Wave
1) If during propagation of a progressive wave, the particles of the medium perform Simple Harmonic Motion about their mean position, then the waves is known as a Harmonic progressive wave.
2) Suppose a plane simple harmonic wave travels from the origin along the positive direction of x – axis from left to the right as shown in below figure.
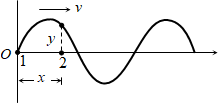
The displacement y of a particle (1) at O from its mean position at any time t is given by: y = a sinωt. The wave reaches the particle 2 after time, \(t=\frac{x}{v}\). Hence, displacement y of a particle (2) is given by:
\(y=a\sin \left( t-\frac{x}{v} \right)=a\sin \left( \omega t-kx \right)\) \(\left( \because \,\,k=\frac{\omega }{v} \right)\),
3) The general equation of a plane progressive wave with initial phase is:
y (x, t) = a sin (ωt ± kx ± φ₀)
Where, y = Displacement; a = Amplitude; ω = Angular Frequency; k = Propagation Constant; φ₀ = Initial Phase and x = Position
4) Particle velocity: The rate of change of displacement y with respect to time t is known as particle velocity. Hence, from y = a sin (ωt – kx).
Particle Velocity \(({{v}_{p}})=\frac{\partial y}{\partial t}=a\omega \cos \left( \omega t-kx \right)\); Maximum particle velocity (vp)max = aω
Also, \(\frac{\partial y}{\partial t}=-\frac{\omega }{k}\times \frac{\partial y}{\partial x}\Rightarrow {{v}_{p}}=-v\times \) Slope of wave at that point.
