Equation of a Plane in Normal Form and Cartesian Form

Equation of a Plane in Normal Form and Cartesian Form

Plane: A plane is a surface such that if any two points are taken on it, the line segment joining them lies completely on the surface.

A plane is determined uniquely if.

• The normal to the plane and its distance from the origin is given, i.e., the equation of a plane in normal form.
• It passes through a point and is perpendicular to a given direction.
• It passes through three given non – collinear points.

Equation of a Plane in Normal Form:

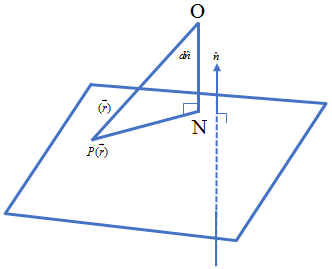
Consider a plane whose perpendicular distance from the origin is d (d ≠ 0). If \(\overrightarrow{ON}\) is the normal form the origin to the plane, and  is the unit normal vector along  \(\overrightarrow{ON}\), then  \(\overrightarrow{ON}=d\hat{n}\).

Let P be any point on the plane. Therefore, \(\overrightarrow{NP}\) is perpendicular to \(\overrightarrow{ON}\).

\(\because \overrightarrow{NP} . \overrightarrow{ON}=0\) … (i)

Let \(\vec{r}\) be the position vector of the point P. Then \( \overrightarrow{NP}=\vec{r}-d\hat{n} \left( as \, \overrightarrow{ON}+\overrightarrow{NP}=\overrightarrow{OP} \right)\),

Therefore, (i) becomes

\(\left( \vec{r}-d\hat{n} \right).d\hat{n}=0\),

\(\left( \vec{r}-d\hat{n} \right).\hat{n}=0\ \ \ \ \left( d\ne 0 \right)\),

\(\left( \vec{r}.\hat{n} \right)-d\hat{n}.\hat{n}=0\),

\(\vec{r}.\hat{n}=d (\because \ \hat{n}.\hat{n}=1)\) … (ii)

This is the vector from of the equation of the plane.

Cartesian Form:  Equation (ii) given the vector equation of a plane, where \(\hat{n}\) is the unit vector normal to the plane.

Let P (x, y, z) be any point on the plane. Then \(\overrightarrow{OP}=\vec{r}=x\hat{i}+y\hat{j}+z\hat{k}\),

Let l, m and n be the direction cosines of . Then \(\hat{n}=l\hat{i}+m\hat{j}+n\hat{k}\),

Therefore, (ii) gives \((x\hat{i}+y\hat{j}+z\hat{k})(l\hat{i}+m\hat{j}+n\hat{k})=d\),

lx + my + nz = d.

This is the Cartesian of the plane in the normal form.