Entropy
Thermodynamics is the study of Energy, Equilibrium and Entropy
The first law of thermodynamics was stated in terms of cycles first and it was shown that the cyclic integral of heat is equal to the cyclic integral of work. When the first law was applied for thermodynamic processes, the existence of a property, the internal energy, was found. similarly, the second law was also first stated in terms of cycles executed by systems. When applied to processes, the second law also leads to the definition of a new property, known as entropy. If the first law is said to be the law of internal energy, then the second law may be stated to be the law of entropy.
Property of Entropy: Let a system be taken from an initial equilibrium state i to a final equilibrium state f by following the reversible path R₁. The system is brought back from f to i by following another reversible path R₂. Then the two paths R₁ and R₂ together constitute a reversible cycle.
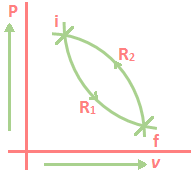
From Clausius Theorem,
\(\oint_{{{R}_{1}}{{R}_{2}}}{\frac{dQ}{T}}\,=\,0\)
The above integral may be replaced as the sum of two integrals, one for path R₁.
\(\underset{{{R}_{1}}}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\,+\,\underset{{{R}_{2}}}{\mathop{\int_{f}^{i}{\frac{dQ}{T}}}}\,\,=\,0\)
Or \(\underset{{{R}_{1}}}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\,=\,-\underset{{{R}_{2}}}{\mathop{\int_{f}^{i}{\frac{dQ}{T}}}}\,\)
Since R₂ is a reversible path
\(\underset{{{R}_{1}}}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\,=\,\underset{{{R}_{2}}}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\)
Since R₁ and R₂ represent any two reversible paths, \(\underset{R}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\) is independent of the reversible path connecting i and f. Therefore, there exists a property of a system whose value at the final state f minus its value at the initial state i is equal to \(\underset{R}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\). This property is called entropy and is denoted by S. If Sᵢ is the entropy at the initial state i and Sf is the entropy at the final state f, then
\(\underset{R}{\mathop{\int_{i}^{f}{\frac{dQ}{T}}}}\,\,=\,{{S}_{f}}\,-\,{{S}_{i}}\) … (1)
When the two equilibrium states are infinitesimally near
\(\frac{d{{Q}_{R}}}{T}\,=\,dS\) … (2)
Where dS is an exact differential because S is a point function and a property. The subscript R in dQ is transferred reversibly.
The word ‘entropy’ was first used by Clausius, taken from the Greek word ‘tropee’ meaning ‘transformation’. It is an extensive property and has the unit J/ K. The specific entropy
\(s\,=\,\frac{S}{m}\,J/kg\,K\)
Applications of Entropy Principle:
⇒ The principle of increase of entropy is one of the most important laws of physical science.
⇒ It is the quantitative statement of the second law of thermodynamics.
⇒ Every irreversible process is accompanied by entropy increase of the universe and this entropy increase quantifies the extent of irreversibility of the process.
⇒ The higher the entropy increases of the universe, the higher will be the irreversibility of the process.
