Energy Stored in a Capacitor
A capacitor is a device for storing energy. When we connect a battery across the two plates of a capacitor, it gets charged. The potential difference gradually increases across the two plates and the battery had to do more work to deliver the same amount of charge due to the continuous increase in potential difference.
While capacitor is connected across a battery, charges come from the battery and get stored in the capacitor plates. But this process of energy storing is step by step only. At the very beginning, capacitor does not have any charge or potential. i.e. V = 0 Volts and q = 0 Coulomb’s.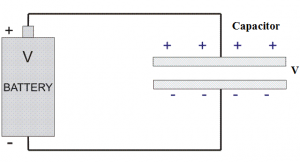
Now at the time of switching, full battery voltage will fall across the capacitor. A positive charge (q) will come to the positive plate of the capacitor, but there is no work done for this first charge (q) to come to the positive plate of the capacitor from the battery. It is because of the capacitor does not have own voltage across its plate, rather the initial voltage is due to the battery.
First charge glows little amount of voltage across the capacitor plates, and then second positive charge will come to the positive plate of the capacitor, but gets replaced by the first charge. As the battery voltage is more than the capacitor voltage then this second charge will be stored in the positive plate. At that condition a little amount of work is to be done to store second charge in the capacitor. Again for the third charge, same phenomenon will appear. Gradually charges will come to be stores in the capacitor against pre- stored charges and their little amount of work done grows up.
Charge will flow from battery to the capacitor plate until the capacitor gains as same potency as the battery. So, we have to calculate the energy of the capacitor from the very beginning to the last moment of charge getting full.
Suppose, a small charge q is stored in the positive plate of the capacitor with respect to the battery voltage V and a small work done is dW. Then considering the total charging time, we can write that,
\(\int\limits_{0}^{W}{dW}=\int\limits_{0}^{Q}{V\,.\,dQ}\)
\(W=\int\limits_{0}^{Q}{\frac{q}{C}}\,.\,dq\left[ \because \,\,C=\frac{q}{V} \right]\)
W = ½ Q²/C
W = ½ CV²
Now, we go for the energy loss during the charging time of a capacitor by a battery. As the battery is in the fixed voltage the energy loss by the battery always follows the equation W = Vq, this equation is not applicable for the capacitor as it does not have the fixed voltage from the very beginning of charging by the battery.
Now, the charge collected by the capacitor from the battery is, Wcapacitor = ½ CV² = ½ QV
Now, the charge lost by the battery is, WIoss = V.Q – ½ QV = QV/2.
This half energy from total amount of energy goes to the capacitor and rest half of energy automatically gets lost from the battery.