Energy of Projectile
A body which is in flight through the atmosphere under the effect of gravity alone and is not being propelled by any fuel is called projectile. If the force acting on a particle is oblique with initial velocity then the motion of particle is called projectile motion.
When a projectile moves upwards its kinetic energy decreases, potential energy increases but the total energy always remains constant. If a body is projected with initial kinetic energy\(K.E\left( =\frac{1}{2}m{{v}^{2}} \right)\), with angle of projection \(\theta \) with the horizontal then at the highest point of trajectory.
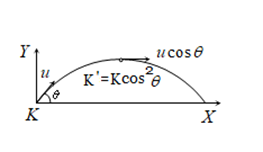
1) Kinetic Energy (K.E) = \(\frac{1}{2}m{{\left(
u\cos \theta \right)}^{2}}=\frac{1}{2}m{{u}^{2}}{{\cos }^{2}}\theta \)
2) Potential Energy (P.E) = \(mgH=mg\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g}=\frac{1}{2}m{{u}^{2}}{{\sin }^{2}}\theta =K{{\sin }^{2}}\theta \) \(\left( As\,\,H=\frac{{{u}^{2}}{{\sin }^{2}}\theta }{2g} \right)\)
3) Total Energy (T.E) = Kinetic Energy + Potential Energy
Total Energy \(=\frac{1}{2}m{{u}^{2}}{{\cos }^{2}}\theta +\frac{1}{2}m{{u}^{2}}{{\sin }^{2}}\theta =\frac{1}{2}m{{u}^{2}}\)
Total Energy \(=\frac{1}{2}m{{u}^{2}}=\) Energy at the point of projection
This is in accordance with the law of conservation of energy.
