Electric Potential

Electric Potential

The electric potential at any point in an electric field is equal to the amount of work done per unit positive test charge or in bringing the unit positive test charge from infinite to that point against the electrostatic force without acceleration. Electric potential is a scalar quantity, it is denoted by V.

\(Electric\,\,Potential(V)\,\,=\,\,\frac{Work\,\,done(W)}{Ch\arg e(q)}\).

Its SI unit is Volts (V) and 1V = 1 J/ C, its dimensional formula is [ML²T⁻³A⁻¹].

Types of Electric Potential: According to the nature of charge potential is of two types.

i. Positive Potential: Due to positive charge.

ii. Negative Potential: Due to negative charge.

Electric Potential of a System of Point Charges: Consider P is a point at which net electric potential is to be determined due to several charges. So net electric potential at P.

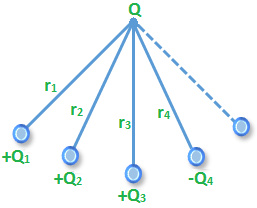
\(Electric\,\,Potential\left( V \right)\,\,=\,\,k\frac{{{Q}_{1}}}{{{r}_{1}}}+k\frac{{{Q}_{2}}}{{{r}_{2}}}+k\frac{{{Q}_{3}}}{{{r}_{3}}}+k\frac{(-{{Q}_{4}})}{{{r}_{4}}}\).

In general,

\(Electric\,\,Potential\left( V \right)\,\,=\,\,\sum\limits_{i=1}^{x}{\frac{k{{Q}_{i}}}{{{r}_{i}}}}\).

It is a state dependent function as electric forces are conservative forces. Electric potential due to a point charge q lying at a distance r from it is given by

\(Electric\,\,Potential\left( V \right)\,\,=\,\,\frac{1}{4\pi {{\varepsilon }_{o}}}\times \frac{q}{r}\).