Electric Field
The force felt by a unit positive charge or test charge when its kept near a charge is called Electric Field. It is also defined as the region which attracts or repels a charge. The electric field is a vector quantity and it is denoted by E. the standard units of the electric field is N/C.
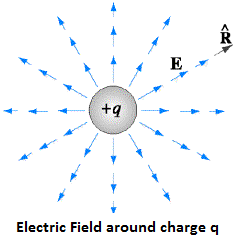
If a charge q is placed in a system, then at a distance r at some point P, electric field is given as:
\(E\,\,=\,\,\frac{kq}{{{r}^{2}}}\widehat{r}\).
Where,
r̂ = Unit Vector = r/r = 1
The Electric field explains how electric force varies with position. The above equation can be written as:
\(E\,\,=\,\,\frac{kq(+1)}{{{r}^{2}}}\widehat{r}\).
This proves electric field is actually the force between a unit positive charges also called test charge. The concept of field was first proposed by Faraday.
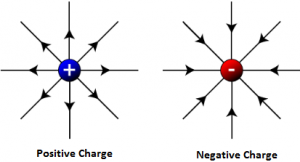
If the electric field is positive, then its direction is radially outward, and if the electric field is negative, then its direction is radially inward. The electric field is also called as Electric field Intensity or Electric field strength as it determines the strength of electric field.
How to find the Electric Field?
Problem: A charge q of 2C is kept stationary in a system. What will be the electric field produced by the charge q at a distance of 3m from it?
Solution: Given,
Charge (q) = 2C
Distance (r) = 3m
We know that:
Electric field produced by charge q:
\(E\,\,=\,\,\frac{kq}{{{r}^{2}}}\widehat{r}\),
\(E\,\,=\,\,9\times {{10}^{9}}\times \frac{2}{{{3}^{2}}}\,\,=\,\,2\times {{10}^{9}}\),
∴ E = 2 x 10⁹ N/C
