Electric Field outside the Spherical Shell
The force felt by a unit positive charge or test charge when its kept near a charge is called Electric Field. It is also defined as the region which attracts or repels a charge. The electric field is a vector quantity and it is denoted by E. the standard units of the electric field is N/C.
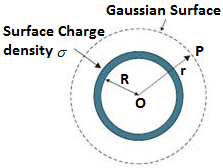
To evaluate the electric field outside the spherical shell, we take point P outside the shell at a distance r from the centre of the spherical shell. By symmetry, we take Gaussian spherical surface with radius r and centre O. The Gaussian surface will pass through P, and experience a constant electric field \(\overrightarrow{E}\) all around as all points is equally distanced “r” from the centre of the sphere.
Then, According to Gauss’s Law:
\(\phi =\frac{q}{{{\varepsilon }_{0}}}\).
The enclosed charge inside the Gaussian surface q will be σ x 4πr². The total electric flux through the Gaussian surface will be:
φ = E x 4πr²
Then, by Gauss’s Law we can write:
\(E\times 4\pi {{r}^{2}}=\sigma \times \frac{4\pi {{R}^{3}}}{{{\varepsilon }_{0}}}\).
\(E=\frac{\sigma {{R}^{2}}}{{{\varepsilon }_{0}}{{r}^{2}}}\).
Now, putting the value of surface charge density σ as\(\frac{q}{4\pi {{R}^{2}}}\), the electric field will become:
\(E=\frac{kq}{{{r}^{2}}}\).
We can write this in vector form as,
\(\overrightarrow{E}\,\,=\,\,\frac{kq}{{{r}^{2}}}\widehat{r}\).
Where,
\(\widehat{r}\) = Radius vector.
If the surface charge density σ is negative, then the direction of the electric field will be radially inward.