This apparent change in frequency of the wave it due to motion of the source or the observer is called Doppler Effect d.
Observer Stationary and Source Moving: Now suppose the observer is at rest with respect to the medium and the source moves towards the observer at a speed u which is less than the wave speed v.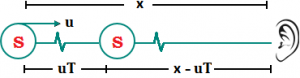 If the frequency of vibration of the source is v₀, it sends compression pulses at a regular interval of \(T=\frac{1}{{{v}_{0}}}\). Suppose the separation between the source and the observer is x when a compression pulse is emitted at t = 0. The next compression pulse will be emitted after a time T. The source will travel a distance uT in this time and hence this second compression wave is emitted from a place which is at a distance x – u, T from the observer. The first pulse takes a time x/v to reach the observer whereas the next one takes \(\frac{\left( x-uT \right)}{v}\).
If the frequency of vibration of the source is v₀, it sends compression pulses at a regular interval of \(T=\frac{1}{{{v}_{0}}}\). Suppose the separation between the source and the observer is x when a compression pulse is emitted at t = 0. The next compression pulse will be emitted after a time T. The source will travel a distance uT in this time and hence this second compression wave is emitted from a place which is at a distance x – u, T from the observer. The first pulse takes a time x/v to reach the observer whereas the next one takes \(\frac{\left( x-uT \right)}{v}\).
Thus, the first compression wave reaches the observer at \({{t}_{1}}=\frac{x}{v}\) and the next compression wave reaches at \({{t}_{2}}=T+\frac{\left( x-uT \right)}{v}\) the time interval between the consecutive compression pulses detected by the observer is, therefore, T’ = t₂ – t₁
= \(T +\frac{x-uT}{v}-\frac{x}{v}=\left( 1-\frac{u}{v} \right)T=\frac{v-u}{v}T\)
The apparent frequency of the sound as experienced by the observer is \(v’=\frac{1}{T’}\)
Or, \(v’=\frac{v}{\left( v-u \right){{v}_{0}}}\) … (1)
Similarly, if the source recedes from the observer at a speed u, the apparent frequency will be \(v’=\frac{v}{\left( v+u \right){{v}_{0}}}\) … (2)
Source Stationary and Observer Moving: Next, consider the case when the source remains stationary with respect to the medium and the observer approaches the source with a speed u.
As the source remains stationary in the medium, compression pulses are emitted at regular interval T from the same point in the medium. These pulses travel down the medium with a speed v and at any instant the separation between two consecutive compression pulses is λ = vT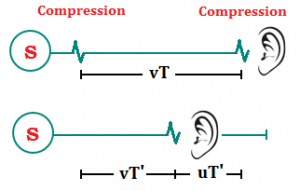 When the observer receives a compression pulse, the next compression pulse (towards the source) is a distance vT away from it. This second compression pulse moves towards the observer at a speed v and the observer moves towards it at a speed u. As a result, the observer will receive this second one wave a time T’ after receiving the first one where
When the observer receives a compression pulse, the next compression pulse (towards the source) is a distance vT away from it. This second compression pulse moves towards the observer at a speed v and the observer moves towards it at a speed u. As a result, the observer will receive this second one wave a time T’ after receiving the first one where
\(T’=\frac{vT}{\left( v+u \right)}\).
The apparent frequency of sound experienced by the observer is then \(v’=\frac{1}{T}\)
Or, \(v’=\left[ \frac{\left( v+u \right)}{v} \right]{{v}_{0}}\) … (3)
Note that, in this case, it is not the same part of air that gives the sensation of pressure variation to the ear at frequency v’. The pressure in any part of the air still oscillates with a frequency v₀ but the observer moves in the medium to detect the pressure of some other part which reaches its maximum a little earlier. Similarly, if the source is stationary in the medium and the observer recedes from it at a speed u, the apparent frequency will be
\(v’=\left[ \frac{\left( v-u \right)}{v} \right]{{v}_{0}}\) … (4)
The equation (1) through (4) may be generalized as
\(v=\left[ \frac{\left( v+{{u}_{0}} \right)}{\left( v-{{u}_{0}} \right)} \right]{{v}_{0}}\) … (5)
