Let f be a relation from A into B then {x ϵ A: (x, y) ϵ R} is codomain of f and {y ϵ B: (x, y) ϵ f} is called range of f
Domain: The domain is input values
Range: The resultant value is called range
Ex: if f = {(a, b), (c, d), (e, f)} then domain f = {a, c, e} and range f = {b, d, f}
Co-domain: The “co-domain” of a function or relation is a set of values that includes the Range as described above, but may also include additional values beyond those in the range
Ex: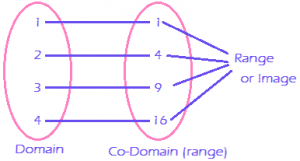
Ex:
Above image having the domain and range the domain is input value and output is range
Example: A simple function like f(x) = x2 can have the domain (what goes in) of just the counting numbers {1, 2, 3, …}, and the range will then be the set {1, 4, 9, …}
Input is {1, 2, 3, …} = domain
Output is {1, 4, 9, …} = range
And another function g(x) = x2 can have the domain of integers {…, -3, -2, -1, 0, 1, 2, 3, …}, in which case the range is the set {0, 1, 4, 9, …}
Domain and range of trigonometric function
| Trigonometric functions | Domain |
Range |
|
sinx |
(-∞, ∞) | [1, -1] |
| cosx | (-∞, ∞) |
[1, -1] |
|
tanx |
R – {(2n + 1)pi/2 | (-∞, ∞) |
| cotx | R – npi |
(-∞, ∞) |
|
cosecx |
R – npi | (-∞,-1] È [1,∞) |
| sec | R – {(2n + 1)pi/2 |
(-∞, -1] È [1, ∞) |
Ex: Find the domain and range of the real function f defined by f(x) = 4 – x/ x – 4
Sol: Given that f(x) = 4 – x/ x – 4
f (x) = – (x – 4)/ (x – 4) take a common”– “
f (x) = -1
The range of f(x) is {-1}
Domain is x – 4 ≠ 0
x ≠ 4
The domain is x ϵ R – {4}
Inverse Function: Let f be defined a function from A to B such that for every element of B their exist a image f, f: A → B is a function then {(y, x)} ϵ B x A : (x, y) ϵ f } is called inverse function.it is denoted by f-1.
Ex: if A = {1, 2, 3} and B = {a, b, c} then f : {(1, c), (2, b), (3, a)} is bijection from A into B and f-1 = {(a, 3), (b, 2), (3, a)} is bijection from B into A.
Let us start with an example:
Here we have the function f(x) = 2x + 3, written as
The Inverse Function goes the other way
So, the inverse of f(x) = 2x + 3 is written
f-1 (y) = \(\frac{\left( y\,-\,3 \right)}{2}\)
Ex: The cool thing about the inverse is that it should give us back the original value:
When the function f turns the apple into a banana. Then the inverse function f-1 turns the banana back to the apple