Here is a brief explanation to know about the distribution of current and voltage in series and parallel connections.
Distribution of current in parallel connection: When all the devices are connected using parallel connections, the circuit is referred to as a parallel circuit. In a parallel circuit, each device is placed in its own separate branch. The presence of branch lines means that there are multiple pathways by which charge can traverse the external circuit.
When resistors are connected in parallel, the potential difference across them is equal and current gets divided in inverse ratio of their resistance. Because i = V/R where, i is the current, V is the voltage and R is the resistance.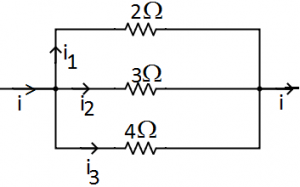
And for parallel circuit V remain same so i α V/R
For Example: i₁ : i₂ : i₃ = ½ : ⅓ : ¼ = 6 : 4 : 3
so \({{i}_{1}}=\frac{6i}{6+4+3}=\frac{6i}{13};\,{{i}_{2}}=\frac{4i}{6+4+3}=\frac{4i}{13};\,{{i}_{3}}=\frac{3i}{6+4+3}=\frac{3i}{13}\).
Distribution of potential in series circuit: When resistors are connected in series, the current through is same and potential is distributed in the ratio of their resistances because V = iR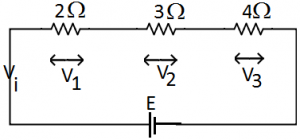
And for same i, i α V/R
For example, V₁ : V₂ : V₃ = 2 : 3 : 4
So, \({{V}_{1}}=\left( \frac{2}{2+3+4} \right)V=\frac{2V}{9}\).
\({{V}_{2}}=\left( \frac{3}{2+3+4} \right)V=\frac{3V}{9};\,{{V}_{3}}=\left( \frac{4}{2+3+4} \right)V=\frac{4V}{9}\).
Finding out equivalent emf of more than one dissimilar cells connected in parallel: Suppose n number of cells having emf’s E₁, E₂ … En and their internal resistances are r₁, r₂ … rn are connected in parallel as shown. The complete network can be replaced by a single source of emf Eeq and internal resistance req.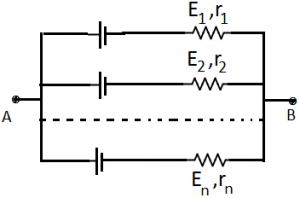
\({{E}_{eq}}=\frac{\frac{{{E}_{1}}}{{{r}_{1}}}+\frac{{{E}_{2}}}{{{r}_{2}}}+…+\frac{{{E}_{n}}}{{{r}_{n}}}}{\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+…\frac{1}{{{r}_{n}}}}=\left[ \sum{\frac{{{E}_{t}}}{{{r}_{t}}}} \right]{{\left[ \sum{\frac{1}{{{r}_{t}}}} \right]}^{-1}}\).
And \(\frac{1}{{{r}_{eq}}}=\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+…\frac{1}{{{r}_{n}}}\).
Or \({{r}_{eq}}={{\left[ \sum{\frac{1}{{{r}_{t}}}} \right]}^{-1}}\).
For two cells in parallel \({{E}_{eq}}=\frac{{{E}_{1}}{{r}_{2}}+{{E}_{2}}{{r}_{1}}}{{{r}_{1}}+{{r}_{2}}}\).
or \({{r}_{eq}}=\frac{{{r}_{1}}{{r}_{2}}}{{{r}_{1}}+{{r}_{2}}}\).
Please note that positive terminals of all the cells are at one point and negative terminals at other common point. If some of the cells are oppositely connected then,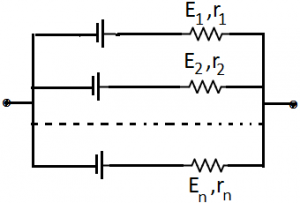
\({{E}_{eq}}=\frac{\frac{{{E}_{1}}}{{{r}_{1}}}-\frac{{{E}_{2}}}{{{r}_{2}}}+…+\frac{{{E}_{n}}}{{{r}_{n}}}}{\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+…+\frac{1}{{{r}_{n}}}}\).
\(\frac{1}{{{r}_{eq}}}=\frac{1}{{{r}_{1}}}+\frac{1}{{{r}_{2}}}+…\frac{1}{{{r}_{n}}}\).