The locus of the point of intersection of the tangents which are at right angles is known as the director circle of the hyperbola.
\(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{^{2}}}}=1\).
The equation to the director circle is x² + y² = a² – b².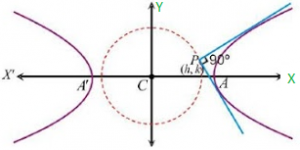
Example: Hyperbola 9x² – 16y² = 144 then find the equation of the director circle.
Solution: The given equation of the hyperbola is 9x² – 16y² = 144
\(\frac{9{{x}^{2}}}{144}-\frac{16{{y}^{2}}}{144}=1\).
\(\frac{{{x}^{2}}}{16}-\frac{{{y}^{2}}}{9}=1\).
Where a² = 16
a = 4
b² = 9
b = 3
The equation of the director circle is x² + y² = a² – b².
We can substitute a, b value above formula
x² + y² = 16 – 9
x² + y² = 7.