Differentiability at a Point
Let f(x) be a real valued function defied on an open interval (a, b) and let c ϵ (a, b). Then f(x) is said to be differentiable or derivable at x = c, if \(\underset{x\to c}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\) exist finitely.
This limit is called the derivative or differential coefficient of the function f(x) at x = c, and is denoted fˈ (c) or Df (c) or \({{\left( \frac{d}{dx}f\left( x \right) \right)}_{x=\ c}}\).
Thus, f(x) is differentiable at x = c
⇒ \(\underset{x\to c}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\),
⇒ \(\underset{x\to {{c}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}=\underset{x\to {{c}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\),
⇒ \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( c-h \right)-f\left( c \right)}{-h}=\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( c+h \right)-f\left( c \right)}{h}\),
The limit \(\underset{x\to {{c}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\) or \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( c-h \right)-f\left( c \right)}{-h}\) is called the left hand derivative of f(x) at x = c and is denoted by fˈ(cˉ) or, Lfˈ(c), while \(\underset{x\to {{c}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( c \right)}{x-c}\) or \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( c+h \right)-f\left( c \right)}{h}\) is called the right hand derivative of f(x) at x = c and is denoted by fˈ(c⁺) or Rfˈ(c).
Thus, f(x) is differentiable at x = c ⇒ Lfˈ (cˉ) = Rfˈ(c). If Lfˈ(cˉ) ≠ Rfˈ(c), we say that f(x) is not differentiable at x = c.
Meaning of differentiability of a function at a point: f(x) is differentiable at point P, if there exists a unique tangent at point P. in order words, f(x) is differentiable at a point P if the curve does not have P as a corner point.
Consider the function f(x) = |x|. This function is not differentiable at x = 0, because if we draw tangent at the origin as the limiting position of the chords on the left hand side of the origin, it is the line y=-x whereas the tangent at the origin as the limiting position of the chords on the right hand side of the origin is the line y = x. mathematically, left hand derivative at the origin is – 1 (slope of the line y = -x) and the fight hand derivate at the origin is 1 (slope of the line y = x).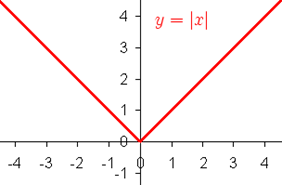
Let f(x) be a differentiable function at a point P. then the curve y = f(x) has a unique tangent at P. since tangent at P is the limiting position of the chord PQ when Q → P. So, if f(x) is differentiable at a point P, then chords exist on both sides of P. consequently f(x) is continuous at P.
It follows from the above discussion that, if a function is not differentiable at x = c, then either it has (c, f(c)) as a corner point or it is discontinuous at x = c.
Also, every differentiable function is continuous.
Relation between Continuity and Differentiability: In the above discussion, we have observed that if a function is differentiable at a point, then it should be continuous at that point and a discontinuous function cannot be differentiable. This fact is provided in the following theorem.
If a function I differentiable at a point, it is necessarily continuous at that point. But the converse is not necessarily true.
OR
f(x) is differentiable at x = c → f(x) is continuous at x = c.
Converse: The converse of the above theorem is not necessarily true i.e. a function may be continuous at a point but may not be differentiable at that point because f(x) = |x| is continuous at x = 0 but it is not differentiable at x = 0.
Evaluate: show that f(x) = |x| is not differentiable at x = 0.
Solution: we have,
(LHD at x = 0)
= \(\underset{x\to {{0}^{-}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( 0-h \right)-f\left( 0 \right)}{0-h-0}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( 0-h \right)-f\left( 0 \right)}{-h}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{\left| h \right|-\left| 0 \right|}{-h}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{\left| -h \right|}{-h}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{h}{-h}=\underset{h\to 0}{\mathop{\lim }}\,-1=-1\),
= \(\underset{x\to {{0}^{+}}}{\mathop{\lim }}\,\frac{f\left( x \right)-f\left( 0 \right)}{x-0}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{f\left( h \right)-f\left( 0 \right)}{h}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{\left| h \right|-\left| 0 \right|}{h}\),
= \(\underset{h\to 0}{\mathop{\lim }}\,\frac{h}{h}=\underset{h\to 0}{\mathop{\lim }}\,1=1\).
∴ (LHD at x = 0) ≠ (RHD at x = 0).
So, f(x) is not differentiable at x = 0.