Different Circles and Centers Connected with Triangle – Part1
Circumcircle and Circumcenter:
The circle passing through the angular point of Triangle ABC is called its circumcenter. The center of this circle is the point of intersection of the perpendicular bisectors of the sides and is called the circumcenter. its radius is denoted by R.
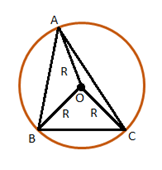
Circumcenter of an acute angled triangle lies inside the triangle.
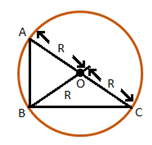
Circumcenter of an obtuse angled triangle lies outside the triangle.
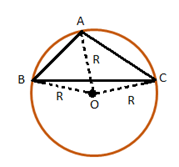
Circumcenter of an right-angled triangle is the mid-point of the hypotenuse.
Distance of the circumcenter from the sides
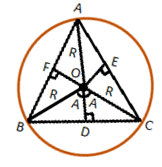
At the circumcenter, the perpendicular bisectors of the sides are concurrent.
Also, \(\angle BOC=2\angle BAC=2A\). Triangles BOD and COD are congruent.
Hence, \(\angle BOD=A\),
Now, in triangle BOD, \(\cos A=\frac{OD}{OB}=\frac{OD}{R}\),
\(OD=R\cos A\),
Similarly, OE = R cosB and OF = RcosC.
