Different Circles and Centers Connected with Triangle – Orthocenter
Orthocenter(H) is the point of intersection of the altitudes of a triangle.
Orthocenter (H) of an acute angled triangle lies inside the triangle.
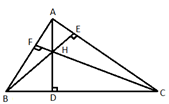
Orthocenter (H) of an obtuse angled triangle lies inside the triangle.
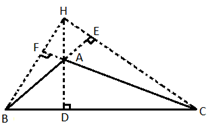
Orthocenter(H) of a right-angled triangle ABC lies at the right angle itself. In fig, the orthocenter H coincide with the right-angle B.
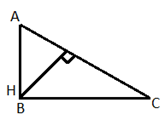
Image if orthocenter(H) in any side of a triangle lies on the circumcircle.
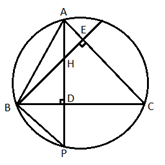
\(\angle HBD=\angle EBC=\left( \frac{\pi }{2} \right)-C\),
\(\Rightarrow \angle BHD=C\),
\(Also,\ \ \angle BPD=\angle BPA=\angle BCA=C\),
\(Thus,\ \ \Delta BPD\ \ and\ \ \Delta BHD\ \ are\ \ congruent\),
⇒ HD = DP
⇒ P is image in H in BC.
