Dielectric in an Electric Field
Suppose a slab of dielectric material is placed in a uniform electric field \(\overrightarrow{{{E}_{0}}}\) set up between the parallel plates of a charged capacitor. The slab becomes electrically polarized. That is, its molecules become electric dipoles oriented in the direction of the field. The net effect is the appearance of negative charge on one face of the slab and an equal positive charge on the opposite face. The net charge in the interior of the slab remains zero. The polarization charges induced on the two faces of the slab produce their own electric field \(\overrightarrow{{{E}_{0}}^{‘}}\), which opposes the external field \(\overrightarrow{{{E}_{0}}}\). Hence, the resultant field \(\overrightarrow{E}\) with in the dielectric is smaller than E₀, but it points in the same direction as \(\overrightarrow{{{E}_{0}}}\).
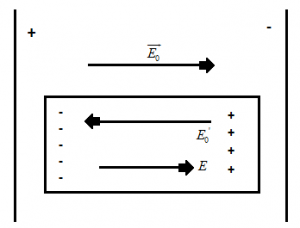
The field in the rest of the free space is still \(\overrightarrow{{{E}_{0}}}\). Hence, we conclude that when a dielectric is placed in an electric field, the field within the dielectric is weekend. The weakening of electric field within the dielectric is illustrated in above figure.
The reduction in the magnitude of the electric field from E₀ to E causes a reduction in the potential difference between the plates of the capacitor. Let V₀ and V be the potential difference with and without the plates, then we have
\(\frac{{{E}_{0}}}{E}=\frac{{{V}_{0}}}{V}\) (∵ E = V/ d).
But, \(\frac{{{V}_{0}}}{V}=\frac{C}{{{C}_{0}}}=K\).
Where,
K = Dielectric constant of the slab.
So, E₀/ E = K
E = E₀/ K
Thus, the electric field with in the dielectric is reduced by factor K.
