In a fluid, at a point, density ρ is defined as: ρ = limΔV → 0 Δm/ΔV = dm/dV.
(1) In case of homogenous isotropic substance, it has no directional properties, so is a scalar.
(2) It has dimensions [ML-3] and S.I. unit kg/m3 while C.G.S. unit g/cc with 1g /cc = 103kg/m3
(3) Density of substance means the ratio of mass of substance to the volume occupied by the substance while density of a body means the ratio of mass of a body to the volume of the body. So for a solid body.
Density of body = Density of substance
While for a hollow body, density of body is lesser than that of substance [As Vbody > Vsub]
(4) When immiscible liquids of different densities are poured in a container the liquid of highest
density will be at the bottom while that of lowest density at the top and interfaces will be plane.
(5) Sometimes instead of density we use the term relative density or specific gravity which is defined as:
RD = Density of body / Density of water
(6) If m₁ mass of liquid of density ρ₁ and m₂ mass of density ρ₂ are mixed, then as
m = m₁ + m₂ and V = (m₁/ ρ₁) + (m₂/ ρ₂) [As V = m/ρ]
ρ = m/V = (m₁ + m₂)/ (m₁/ ρ₁) + (m₂/ ρ₂) = ∑mᵢ/ ∑ (mᵢ/ρᵢ)
If m₁ = m₂ ρ = 2ρ₁ρ₂/ (ρ₁ + ρ₂) = Harmonic mean
(7) If V₁ volume of liquid of density ρ₁ and V₂ volume of liquid of density ρ₂ are mixed, then as:
m = ρ₁ V₁ + ρ₂ V₂ and V = V₁ + V₂ [As ρ = m/V]
If V₁ = V₂ = V ρ = (ρ₁ + ρ₂)/ 2 = Arithmetic Mean
(8) With rise in temperature due to thermal expansion of a given body, volume will increase while mass will remain unchanged, so density will decrease, i.e.
ρ/ ρₒ = (m/ V)/ (m/ Vₒ) = Vₒ/V = Vₒ/ Vₒ (1 + γΔθ) [As V = Vₒ (1 + γΔθ)]
Or ρ = ρₒ/ (1 + γΔθ) ≈ ρₒ (1 – γΔθ)
(9) With increase in pressure due to decrease in volume, density will increase, i.e.,
ρ / ρₒ = (m/ V)/ (m/ Vₒ) = Vₒ/V [As ρ = m/ V]
But as by definition of bulk-modulus
B = – Vₒ Δp/ ΔV i.e., V = Vₒ [1 – (Δp/B)]
So, ρ = ρₒ [1 – (Δp/B)¯¹] ≈ ρₒ [1 + (Δp/B)]
Problem: A homogeneous solid cylinder of length (L<H/ 2). Cross-sectional area A/5 is immersed such that it floats with its axis vertical at the liquid-liquid interface with length L/4 in the denser liquid as shown in the fig. The lower density liquid is open to atmosphere having pressure Pₒ. Then density D of solid.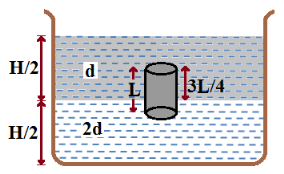
(a) 5/4 d
(b) 4/5 d
(c) Ad
(d) d/5
Solution: (a):
Weight of cylinder = up thrust due to both liquids
V x D x g = (A/5 x ¾ L) x d x g + (A/5 x L/4) x 2d x g
Þ (A/5 x L) D x g = (A x L x d x g)/ 4
Þ D/5 = d/4
∴ D = 5/4 d