In classical mechanics, a constraint is a relation between coordinates and momenta (and possibly higher derivatives of the coordinates).
In other words, a constraint is a restriction on the freedom of movement of a system of particles.
The only difference between a constraint equation and eg a conservation equation is that a conservation equation is physics, but a constraint equation is geometry.
With example, a system of three pulleys at heights p q and r, we get physics equations (usually F = ma) for each pulley, but the “a” in F = ma is different for each pulley (in fact, its p, q and r respectively).
So we need a geometric equation relating p, q and r.
Usually this simply tells us the length of the string in terms of p, q and r.
Since we know that that length is constant, we can differentiate once (or twice) to get a neat “constraint equation”.
The following are different examples of Constraint Relations.
Two masses tied to a string going over a friction less pulley m₁ > m₂.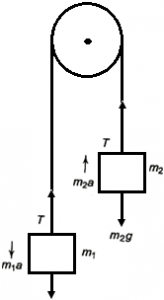
If ‘a’ is the common acceleration of the masses and ‘T’ the tension in the string, then, for mass m₁.
T – m₁g = -m₁a
T = m₁ (g – a) … (i)
Similarly for mass m₂, the net force T – m₂g = m₂a which gives
T = m₂ (g + a) … (ii)
From Eqn. (i) and (ii) we get,
\(a=\frac{({{m}_{1}}-{{m}_{2}})g}{({{m}_{1}}+{{m}_{2}})}\).
And \(T=\frac{2{{m}_{1}}{{m}_{2}}}{({{m}_{1}}+{{m}_{2}})}g\).
Two masses in contact: Two masses m₁ and m₂ in contact placed on a horizontal frictionless surface. A force F is applied as shown and as a result the masses move with acceleration, which is given by \(a=\frac{F}{({{m}_{1}}+{{m}_{2}})}\).
The force on m₁ is F and the contact force on m₂ is \({{F}_{2}}=\frac{{{m}_{2}}F}{({{m}_{1}}+{{m}_{2}})}\).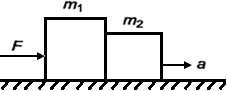
Three masses in contact: If three masses m₁, m₂ and m₃ are placed in contact and force F is applied to mass m₁, the three masses move with acceleration.
\(a=\frac{F}{({{m}_{1}}+{{m}_{2}}+{{m}_{3}})}\).
The force acting on mass m₁ is F. The contact forces acting of masses m2 and m3 respectively are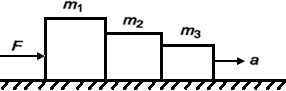
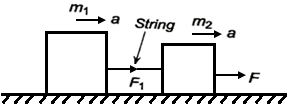\({{F}_{2}}=\frac{({{m}_{2}}+{{m}_{3}})F}{({{m}_{1}}+{{m}_{2}}+{{m}_{3}})}\).
And \({{F}_{3}}=\frac{{{m}_{3}}F}{({{m}_{1}}+{{m}_{2}}+{{m}_{3}})}\).