If no external torque is acting upon a body rotating about an axis, then the angular momentum of the body remains constant, that is,
J = I ω = constant
This is called the ‘law of conservation of angular momentum’. If I decreases, ω increases and vice versa.
Proof: We have read above that when a body rotates about an axis under the action of an external torque τ, then the rate of change of angular momentum of the body is equal to the torque; that is,
\(\frac{dJ}{dt}=\tau \)
If the external torque is zero (τ = 0), then
\(\frac{dJ}{dt}=0\)
Or dJ = 0
Or J = constant.
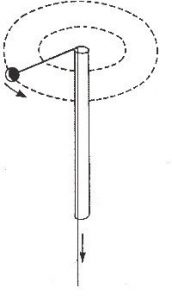
Example 1: Suppose a ball is tied at one end of a cord whose other end passes through a vertical hollow tube. The tube is held in one hand and the cord in the other. The ball is set into rotation in a horizontal circle. If the cord is pulled down, shortening the radius of the circular path of the ball; then the ball rotates faster than before. The reason is that by shortening the radius of the circle, the moment of inertia of the ball about the axis of rotation decreases. Hence, by the law of conservation of angular momentum, the angular velocity of the hall about the axis of rotation increases.
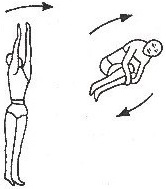
Example 2: When a driver jumps into water from a height, he does not keep his body straight but pulls in his arms and legs towards the centre of his body. On doing so, the moment of inertia I of his body decreases. But since the angular momentum Iω remains constant, his angular velocity ω correspondingly increases. Hence during jumping he can rotate his body in the air.