Conjugate Points and Conjugate Lines

Conjugate Points: Two points P and Q are said to be conjugate points with respect to the circle S = 0 if Q lies on the polar of P.

The condition that the two points P(x₁, y₁) and Q(x₂, y₂) are conjugate points with respect to the circle S = 0 is S₁₂ = 0.
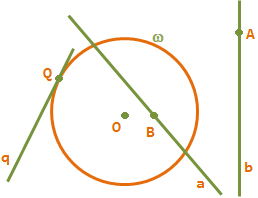
Where A and B are conjugate points, a and b are conjugate lines, Q and q are self-conjugate.

Conjugate Lines:

If P and Q are conjugate points with respect to the circle S = 0 then the polar of P and Q are called conjugate lines with respect to the circle S = 0.
Let x² + y² + 2gx + 2fy + c = 0 be a circle with radius r and l₁x + m₁y + n₁ = 0, l₂x + m₂y + n₂ = 0 are conjugate lines with respect to the circle if r² (l₁l₂ + m₁m₂) = (l₁g + m₁f – n₁ ) (l₂g + m₂f – n₂)

Inverse Points: Let C be the center and be the radius of the circle S = 0. Two points P and Q are said to be inverse points with respect to the circle S = 0 if C, P, Q are collinear such that P, Q are on the same side of C and CP. CQ = r²

Note: The inverse of the point P with respect to the circle S = 0 is the foot of perpendicular from the center of the circle S = 0 to the polar of P.

Example: If (4, k) and (2, 3) are conjugate points with respect to the circle x² + y² = 17 then find k.

Solution: Here (x₁, y₁) = (4, k) and (x₂, y₂) = (2, 3)

And S = x² + y² -17 = 0. Since the given points are conjugate, we have S₁₂ = 0

i.e. x₁x₂ + y₁y₂ -17 = 0

i.e., 4(2) + k (3) – 17 = 0

k = 3.