Condition for Parallel or Perpendicular Lines
When the two lines are perpendicular, the angle between the lines is 90° which gives the condition of perpendicularity as l₁ l₂ + m₁ m₂ + n₁ n₂ = 0 or this implies a₁ a₂ + b₁ b₂ + c₁ c₂ = 0.
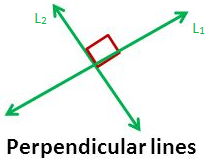
Similarly, when the two lines are parallel, the angle between them i.e. θ = 0.
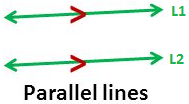
This gives \(\frac{{{l}_{1}}}{{{l}_{2}}}=\frac{{{m}_{1}}}{{{m}_{2}}}=\frac{{{n}_{1}}}{{{n}_{2}}}\)
This also gives \(\frac{{{a}_{1}}}{{{a}_{2}}}=\frac{{{b}_{1}}}{{{b}_{2}}}=\frac{{{c}_{1}}}{{{c}_{2}}}\)
The projection of a line segment on a given line: Suppose we have a line segment joining the points P (x₁, y₁, z₁) and Q(x₂, y₂, z₂), then the projection of this line on another line having direction cosines as l, m, n is AB = l (x₂ – x₁) + m (y₂ – y₁) + n(z₂ – z₁) = 0.
Problems: If the direction of two lines are given by l + m + n = 0 and mn – 2ln + lm = 0, then find the angle between the lines.
Solution: \(\frac{f}{a}+\frac{g}{b}+\frac{h}{c}=0\)
θ = 90
