Let C1, C2 be the centers and r1, r2 be the radii of two circles S = 0 and S’ = 0 respectively. Further \(\overline{{{C}_{1}}{{C}_{2}}}\) represents the line segment from C1 to C2. The following cases arises with regard to the relative position of two circles.
1. C1 + C2 > r1 + r2
In this case the two circles do not intersect and one circle will be away from the other circle.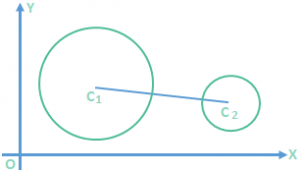
2. C1C2 = r1 + r2
In this case the two circles touch each other externally.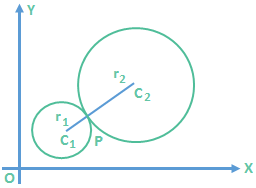
3. |r1 – r2| < C1C2 < r1 + r2
In this case the two circles intersect in two distinct points.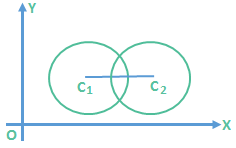
4. C1C2 = |r1 – r2|
The two circles touch each other internally in this case.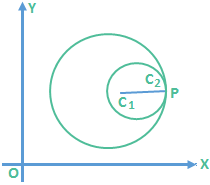
5. C1C2 < |r1 – r2|
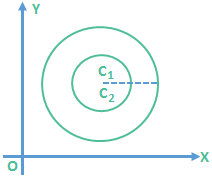
In this case the two circles do not intersect/touch and one circle will be completely inside the other.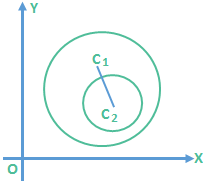
Note: If C1C2 = 0 then the centers of the two circles coincide and they are concentric circles.