Components of a Vector

Components of a Vector

Let us take the points A (1, 0, 0), B (0,1,0) and C(0,0,1) on the X – axis, Y – axis and z – axis, respectively.

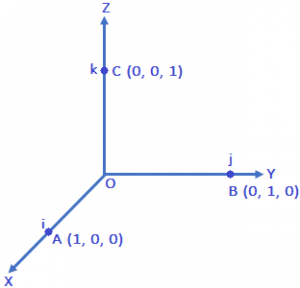
Then, clearly \(\left| \overrightarrow{OA} \right|=1\), \(\left| \overrightarrow{OB} \right|=1\) and \(\overrightarrow{\left| OC \right|}\text{ }=\text{ }1\).

The vector\(\overrightarrow{OA}\), \(\overrightarrow{OB}\) and \(\overrightarrow{OC}\) each having magnitude 1, are called unit vector along the axes OX, OY and OZ, respectively and are denoted by i, j and k respectively.

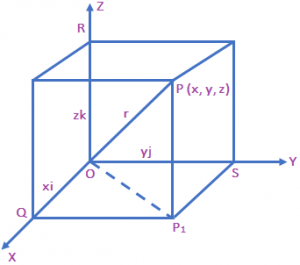
Now, consider the position vector OP of a point P (x, y, z) as shown in fig. let P be the foot of the perpendicular from P on the plane XOY.

We thus, see that P₁P is parallel to the z – axis. As i, j and k are the unit vectors along the x-, y- and x -axes, respectively and by the definition of the coordinates of P, we have P₁P = OR = zk

Similarly, OS = jy and OQ = xi.

Therefore, it follows that OP₁ = OQ + OP₁ = xi + yj + zk

Hence, the position vector of P with reference to O is given by

\(\left| O{{P}_{1}} \right|\text{ }=\sqrt{|\overrightarrow{OQ}{{|}^{2}}+\overrightarrow{Q{{P}_{1}}}{{|}^{2}}}=\sqrt{{{x}^{2}}+{{y}^{2}}}\).

And in the right-angled triangle OP₁P, we have \(\left| \overrightarrow{OP} \right|=\sqrt{|O{{P}_{1}}{{|}^{2}}+|\overrightarrow{{{P}_{1}}P}{{|}^{2}}}=\sqrt{({{x}^{2}}+{{y}^{2}})+{{z}^{2}}}\).

Hence, the length of any vector r = xi + jy + zk is give by \(\left| \overrightarrow{r} \right|=|xi+jy|zk|=\sqrt{{{x}^{2}}+{{y}^{2}}+{{z}^{2}}}\).