Complex Numbers – Equation of a Circle
Equation of a Circle: Consider a fixed complex number zₒ and let z be any complex number which moves in such a way that its distance from zₒ is always to r. this implies z would lie on a circle whose center is zₒ and radius is r. and its equation would be
|z – zₒ| = r
Squaring on both sides
|z – zₒ|² = r²
\((z-{{z}_{0}})(\overline{z}-\overline{{{z}_{0}}})={{r}^{2}}\),
\(z\overline{z}-z\overline{{{z}_{0}}}-\overline{z}{{z}_{0}}+{{z}_{0}}\overline{{{z}_{0}}}-{{r}^{2}}=0\).
Let -a = zₒ and \({{z}_{0}}\overline{{{z}_{0}}}-{{r}^{2}}=b\). Then
\(z\overline{z}+a\overline{z}+\overline{a}z+b=0\).
It represents the general equation of a circle in the complex plane.
Now, let us consider a circle described on a lime segment AB \((A({{z}_{1}}),B({{z}_{2}}))\) as its diameter. Let P(z) be any point on the circle. As the angle in the semicircle is \(\frac{\pi }{2}\), So
\(\angle APB=\frac{\pi }{2}\)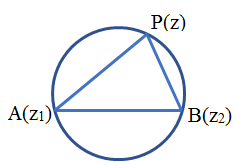
\(\arg \left( \frac{{{z}_{1}}-z}{{{z}_{2}}-z} \right)=\pm \frac{\pi }{2}\),
\(\frac{z-{{z}_{1}}}{z-{{z}_{2}}}\) is purely imaginary
\(\frac{z-{{z}_{1}}}{z-{{z}_{2}}}+\frac{\overline{z}-\overline{{{z}_{1}}}}{\overline{z}-{{\overline{z}}_{2}}}=0\),
\((z-{{z}_{1}})(\overline{z}-\overline{{{z}_{2}}})+(z-{{z}_{2}})(\overline{z}-\overline{{{z}_{1}}})=0\).
