Combination of Cells
A cell is used to maintain current in an electric circuit. We cannot obtain a strong current from a single cell. Hence need arises to combine two or more cells to obtains a strong current. Cells can be combined in two possible ways:
1) Combination of Cells in Series connection:
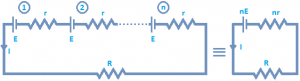
In this combination, cells are so connected that –ve terminal of each cell is connected with the +ve terminal of next and so on. Suppose n cells are connected in this way. Let e.m.f and internal resistance of each cell are E and r respectively.
Net e.m.f of the cells = nE
Total internal resistance = nr
Hence,
Total resistance of the circuit = nr + R
If total current in the circuit is I, then
\(I\,\,=\,\,\frac{Net\,E.M.F}{Total\,resis\tan ce}\,\,=\,\,\frac{nE}{nr+R}\) … (1)
Case (1): If nr << R, then I = nE/R.
That is, if total internal resistance of the cells is far less than external resistance, then current obtained from the cells is approximately equal to n times the current obtained from a single cell. Hence cells, whose total internal resistance is less than external resistance, just be joined in series to obtain strong current.
Case (2): If nr >> R, then \(I\,\cong \,\frac{nE}{nr}\,=\,\frac{E}{r}\).
That is, if total internal resistance of the cells is much greater than the external resistance, then current obtained from the combination of n cells is nearly the same as obtained from a single cell. Hence there is no use of joining such cells in series.
2) Combination of Cells in Parallel:
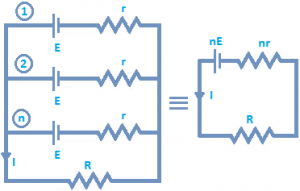
A) When E.M.F’s and internal resistance of all the cells are equal: In this combination, positive terminals of all the cells are connected at one point and negative terminals at other point. Figure shown such cells connected in parallel across some external resistance R. Let e.m.f and internal resistance of each cell are E and r respectively. Because all the cells are connected in parallel between two points,
Hence, e.m.f of battery = E
Total internal resistance of the combination of n cells = r/n
Because external resistance R is connected in series with internal resistance,
Hence, total resistance of the circuit = (r/n) + R
If current in external resistance is I, then \(I\,=\,\frac{Net\,E.M.F}{Total\,resis\tan ce}\,=\,\frac{E}{(r/n)\,+\,R}\,=\,\frac{nE}{r\,+\,nR}\).
Case (1): If r << R, then \(I\,\cong \,\frac{nE}{nR}\,=\,\frac{E}{R}\).
That is, if internal resistance of the cells is much less than external resistance, then total current obtained from the combination is nearly equal to current given by one cells only. Hence there is no use of joining cells of low internal resistance in parallel.
Case (2): If r >> R, then \(I\,\cong \,\frac{nE}{r}\).
That is, if the internal resistance of the cells is much higher than the external resistance, then total current is nearly equal to n times the current given by one cell. Hence cells of high internal resistance must be joined in parallel to get a strong current.
B) When E.M.F’s and Internal Resistance of all the cells connected in parallel are different: In this case, total current in external resistance is obtained with the help of Kirchhoff’s laws. Figure shows three cells of e.m.f E₁, E₂ and E₃ and internal resistances r₁, r₂ and r₃ connected in parallel across some external resistance R. Suppose currents given by three cells are i₁, i₂ and i₃.
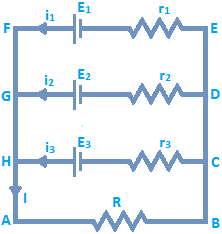
Hence according to Kirchhoff’s first law, total current I in external resistance R, is given by I = i₁ + i₂ + i₃ … (1)
Applying Kirchhoff’s 2nd law to closed mesh ABEF we get,
IR + i₁r₁ = E₁ (or) \({{I}_{1}}\,=\,\left[ \frac{{{E}_{1}}\,-\,IR}{{{r}_{1}}} \right]\) … (2)
\({{i}_{2}}\,=\,\left[ \frac{{{E}_{2}}\,-\,IR}{{{r}_{2}}} \right]\) … (3)
\({{i}_{3}}=\,\left[ \frac{{{E}_{2}}\,-\,IR}{{{r}_{3}}} \right]\) … (4)
Substituting equation (2), (3) and (4) in equation (1), we have:
\(I\,=\,\frac{{{E}_{1}}\,-\,IR}{{{r}_{1}}}\,+\,\frac{{{E}_{2}}\,-\,IR}{{{r}_{2}}}+\frac{{{E}_{3}}-\,IR}{{{r}_{3}}}\),
\(I\,=\,\frac{{{E}_{1}}}{{{r}_{1}}}\,+\,\frac{{{E}_{2}}}{{{r}_{2}}}\,+\,\frac{{{E}_{3}}}{{{r}_{3}}}\,-\,IR\,\times \,\left( \frac{1}{{{r}_{1}}}\,+\,\frac{1}{{{r}_{2}}}\,+\,\frac{1}{{{r}_{3}}} \right)\),
\(I\,\left[ 1+R\left( \frac{1}{{{r}_{1}}}\,+\,\frac{1}{{{r}_{2}}}\,+\,\frac{1}{{{r}_{3}}} \right) \right]\,=\,\frac{{{E}_{1}}}{{{r}_{1}}}\,+\,\frac{{{E}_{2}}}{{{r}_{2}}}\,+\,\frac{{{E}_{3}}}{{{r}_{3}}}\),
\(I\,=\,\frac{\frac{{{E}_{1}}}{{{r}_{1}}}\,+\,\frac{{{E}_{2}}}{{{r}_{2}}}\,+\,\frac{{{E}_{3}}}{{{r}_{3}}}}{1+R\left( \frac{1}{{{r}_{1}}}\,+\,\frac{1}{{{r}_{2}}}\,+\,\frac{1}{{{r}_{3}}} \right)}\),
If n cells are joined in parallel, then \(I\,=\,\frac{\sum{\frac{{{E}_{1}}}{{{r}_{1}}}}}{1\,+\,\sum{\frac{1}{{{r}_{1}}}}}\) and \({{E}_{eq}}\,=\,\frac{\sum{\frac{{{E}_{1}}}{{{r}_{1}}}}}{1\,+\,\sum{\frac{1}{{{r}_{1}}}}}\),
\({{r}_{eq}}\,=\,\frac{1}{\sum{\frac{1}{{{r}_{1}}}}}\).
