Circular Permutations

The number of circular permutation of n distinct objects is (n – 1)!
The number of circular permutation of n things in which clockwise and anti-clockwise arrangements give rise to different permutations is (n – 1)!
If anti clockwise and clockwise order of arrangements are not distinct. Then the number of circular permutations of n distinct items is ½ (n – 1)!.
Example:

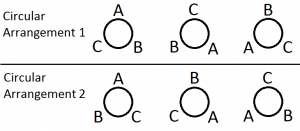
Example: Arrangement of beads in a necklace

Arrangement of flowers in a garland etc.

Example: In how many ways can 8 students be seated in a (i) line (ii) circle

Solution: The number of ways in which 8 students can be seated in a line = ⁸P₈ = 8! = 40320

The number of ways in which 8 students can be seated in a circle = (8 – 1)! = 7!

Example: In how many ways can be seven persons sit around a table so that all that not have the same neighbor in any two arrangements?

Solution: Clearly 7 persons can sit at a round table in (7 – 1)! = 6! Ways. But in clockwise and anticlockwise arrangements each person will have the same neighbors.

So, the required number of ways = ½ (6!) = 360

Example: Find the number of ways in which 10 different beads can be arranged to form a necklace.

Solution: Ten different beads can be arranged in circular form in (10 – 1)! = 9 ways since there is no distinct between the clockwise and anticlockwise arrangements so the required number of arrangements = ½ (9!).