Circles – Power of a Point

Circles – Power of a Point

Let S = 0 be a circle with center C and radius r. let P be a point. Then CP² – r² is called power of P with respect to the circle S = 0.

Theorem: The power of a point P (x₁, y₁) with respect to the circle S = 0 is S₁₁.

Proof: Let S ≡ x² + y² + 2gx + 2fy + c = 0 be the given circle.

Centre C = (-g, -f)

and P (x₁, y₁)

CP = √ [(x₁ + g)² + (y₁ + f)²]

Squaring on both sides

CP² = (x₁ + g)² + (y₁ + f)² … (1)

Radius (r) = √(g² + f² – c)

Squaring on both sides

r² = g² + f² – c … (2)

from equation (1) and (2)

CP² – r²

= (x₁ + g)² + (y₁ + f)² – (g² + f² – c)

= x₁² + 2x₁ g + g² + y₁² + 2y₁f + f² – g² – f² + c

= x₁² + y₁² + 2gx₁ + 2fy₁ + c = 0

S₁₁ = x₁² + y₁² + 2gx₁ + 2fy₁ + c = 0

Let S = 0 be a circle and P be a point. Then

i) P lies inside the circle S = 0 if the power of P is negative.

ii) P lies on the circle S = 0 if the power of P is zero

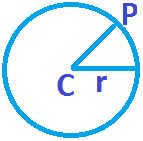
iii) P lies outside the circle S = 0 if the power of P is positive.

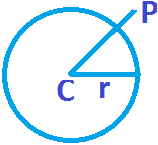
Example: Find the power of (2, 3) with respect to x² + y² – 2x + 2y + 10 = 0

Solution: Given that,

S ≡ x² + y² – 2x + 2y + 10 = 0

Power of point is (2, 3)

we can use the formula S₁₁ = 0

S₁₁ = x₁² + y₁² – 2x₁ + 2y₁ + 10 = 0

Put x₁ = 2, y₁ = 3

S₁₁ = (2) ² + (3) ² – 2(2) + 2(3) + 10 = 0

S₁₁ = 4 + 9 – 4 + 6 + 10 = 0

S₁₁ = 25

Therefore, P lies outside the circle S = 0 if the power of P is positive.