Circles – Midpoint of Chord

The equation of the chord of the circle S = 0 having P (x₁, y₁) as its mid-point is S₁ = S₁₁.

Proof: Let the equation of the circle be S = x² + y² + 2gx + 2fy + c = 0.

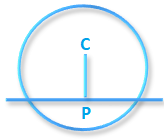
Centre C = (-g, -f) and P (x₁, y₁)

Slope of \(\overleftrightarrow{CP}\) is (y ₁ + f)/ (x ₁ + g)

(since slope(m) = (y₂ – y₁)/ (x₂ – x₁))

Slope of the chord having P as its mid-point is – (x ₁ + g) / (y ₁ + f)

Equation of the chord having P as mid-point is \((y-{{y}_{1}})=-\left( \frac{{{x}_{1}}+g}{{{y}_{1}}+f} \right)(x-{{x}_{1}})\),

⇒ (y – y₁) (y₁ + f) = – (x₁ + g) (x -x₁)

⇒ yy₁ + yf – y₁² – y₁f =- (x₁x – x₁² + gx – gx₁)

⇒x₁² + y₁² + gx₁ + fy₁ = xx₁ + yy₁ + gx + yf

Both sides add gx + yf + c

⇒ x₁² + y₁² + g(x + x₁) + f (y + y₁) + c = xx₁ + yy₁ + 2gx + 2fy + c

⇒ S₁ = S₁₁

Example: Find the equation of the chord of the Circles x² + y² – 4x + 6y – 3 = 0 having (1, -2) as its midpoint.

Solution: Given that x² + y² – 4x + 6y – 3 = 0

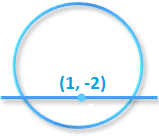
And point P (1, -2)

Required equation is S₁ = S₁₁

x – 2y – 2 (x + 1) + 3 (y – 2) – 3 = (1)² + (-2)² – 4(1) + 6(-2) – 3

⇒ x – 2y – 2x – 2 + 3y – 6 – 3 = 1 + 4 – 4 – 12 – 3

⇒ – x + y + 3 = 0

⇒ x – y – 3 = 0.