Chord of Contact – Ellipse

Chord of Contact – Ellipse

Let PQ and PR be the tangent to the ellipse \(\frac{{{x}^{2}}}{{{a}^{2}}}+\frac{{{y}^{2}}}{{{b}^{2}}}=1\) drawn from any external point P (h, k).

Then QR is called the chord of contact of the ellipse.

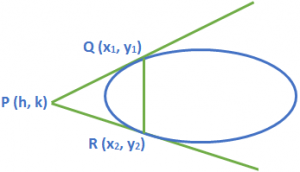
Let Q ≡ (x₁, y₁) and R = (x₂, y₂)

Therefore, the equation of tangents PQ and PR respectively are

\(\frac{x{{x}_{1}}}{{{a}^{2}}}+\frac{y{{y}_{1}}}{{{b}^{2}}}=1\) … (1)

And

\(\frac{x{{x}_{2}}}{{{a}^{2}}}+\frac{y{{y}_{2}}}{{{b}^{2}}}=1\)… (2)

Since equation (1) and (2) pass through P (h, k), we have

\(\frac{h{{x}_{1}}}{{{a}^{2}}}+\frac{k{{y}_{1}}}{{{b}^{2}}}=1\) and

\(\frac{h{{x}_{2}}}{{{a}^{2}}}+\frac{k{{y}_{2}}}{{{b}^{2}}}=1\).

Hence it is clear that Q (x₁, y₁) and R (x₂, y₂) lie on

hx/a² + ky/b² = 1

Or T = 0 which is the chord of contact QR, where

T= hx/a² + ky/b² – 1 = 0

Example: If from a point P, tangents PQ and PR are draw to the ellipse x²/2 + y² = 1 so that the equation of QR is x+3y=1, then find the coordinates of P.

Solution: Let the coordinates of P be (h, k)

Then the equation of QR is xh/2 + ky = 1 … (1)

But is given as

x + 3y = 1 … (2)

Therefore, (1) and (2) are identical

Hence h/2 = k/3 = 1

h = 2 and

K = 3

Therefore, the coordinates of P are (2,3).