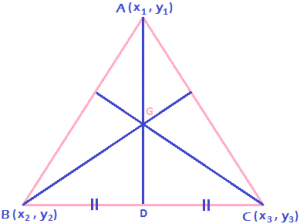
Centroid, Orthocenter, Circumcenter & Incenter of a Triangle
Centroid:
- The centroid of a triangle is the point of intersection of medians. It divides medians in 2 : 1 ratio.
- IfA(x₁,y₁), B(x₂,y₂) and C(x₃,y₃) are vertices of triangle ABC, then coordinates of centroid is \(G=\left( \frac{{{x}_{1}}+{{x}_{2}}+{{x}_{3}}}{3},\,\frac{{{y}_{1}}+{{y}_{2}}+{{y}_{3}}}{3} \right)\).
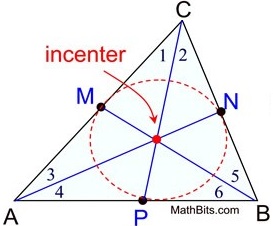
Incenter: Point of intersection of angular bisectors
The incenter is the center of the incircle for a polygon or in sphere for a polyhedron (when they exist). The corresponding radius of the incircle or in sphere is known as the in radius. The incenter can be constructed as the intersection of angle bisectors coordinates of \(I=\left( \frac{a{{x}_{1}}+b{{x}_{2}}+c{{x}_{3}}}{a+b+c},\,\frac{a{{y}_{1}}+b{{y}_{2}}+c{{y}_{3}}}{a+b+c} \right)\)
Where a, b, c are sides of triangle ABC.
 Circumcenter: The circumcenter is the center of a triangle’s circumcircle. It can be found as the intersection of the perpendicular bisectors
Circumcenter: The circumcenter is the center of a triangle’s circumcircle. It can be found as the intersection of the perpendicular bisectors
Point of intersection of perpendicular bisectors
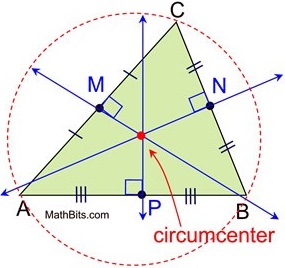 Co-ordinates of circumcenter O is \(O=\left( \frac{{{x}_{1}}\sin 2A+{{x}_{2}}\sin 2B+{{x}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C},\,\frac{{{y}_{1}}\sin 2A+{{y}_{2}}\sin 2B+{{y}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right)\)
Co-ordinates of circumcenter O is \(O=\left( \frac{{{x}_{1}}\sin 2A+{{x}_{2}}\sin 2B+{{x}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C},\,\frac{{{y}_{1}}\sin 2A+{{y}_{2}}\sin 2B+{{y}_{3}}\sin 2C}{\sin 2A+\sin 2B+\sin 2C} \right)\)
Orthocenter: The orthocenter is the point where the three altitudes of a triangle intersect. A altitude is a perpendicular from a vertex to its opposite side
Point of intersection of altitudes of triangle ABC.
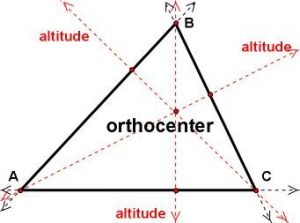 Coordinates of orthocenter H is \(H=\left( \frac{{{x}_{1}}\tan A+{{x}_{2}}\tan B+{{x}_{3}}\tan C}{\tan A+\tan B+\tan C},\,\frac{{{y}_{1}}\tan A+{{y}_{2}}\tan B+{{y}_{3}}\tan C}{\tan A+\tan B+\tan C} \right)\)
Coordinates of orthocenter H is \(H=\left( \frac{{{x}_{1}}\tan A+{{x}_{2}}\tan B+{{x}_{3}}\tan C}{\tan A+\tan B+\tan C},\,\frac{{{y}_{1}}\tan A+{{y}_{2}}\tan B+{{y}_{3}}\tan C}{\tan A+\tan B+\tan C} \right)\)
Important points:
- Orthocenter of a right-angled triangle is at its vertex forming the right angle.
- The orthocenter H, circumcenter O and centroid G of a triangle are collinear and G Divides H, O in ratio 2 : 1 i.e., HG: OG = 2 : 1
