Every physical system has associated with it a certain point whose motion characterises the motion of the whole system. When the system moves under some external forces, then the point moves as if the entire mass of the system is concentrated at this point and also the external force is applied at this point for translation motion. This point is called the center of mass of the system.
Position of Centre of Mass:
(a) System of two particles: Consider first a system of two particles m₁ and m₂ at distances x₁ and x₂ respectively, from some origin O. We define a point C, the centre of mass of the system, as a distance xcm from the origin O, where xcm is defined by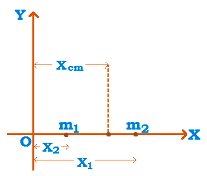
xcm = (m₁ x₁ + m₂ x₂) / m₁ + m₂
xcm can be regarded as mass -weighted mean of x₁ and x₂.
(b) System of many particles
(i) If the particles are distributed in space,
xcm = (∑ mᵢ xᵢ)/ M, ycm = (∑ mᵢ yᵢ)/ M, zcm = (∑ mᵢ zᵢ)/ M.
So, position vector of C is given by \({{\overrightarrow{r}}_{cm}}={{x}_{cm}}\hat{i}+{{y}_{cm}}\hat{j}+{{z}_{cm}}\hat{k}=\frac{\sum{{{m}_{i}}{{{\vec{r}}}_{i}}}}{\sum{{{m}_{i}}}}=\frac{\sum{{{m}_{i}}{{{\vec{r}}}_{i}}}}{M}\)
Example 1: Find the centre of mass of the four point masses as shown in figure.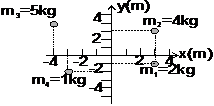
Solution: The total mass M = 12 kg from equation, we have
xcm = [(2kg) (3m) + (4kg) (3m) + (5kg) (- 4m) + (1kg) (- 3m)]/ 12kg = -5/12 m
ycm = [(2kg) (- 1m) + (4kg) (3m) + (5kg) (4m) + (1kg) (- 2m)]/ 12kg = 28/12 m
The position of the cm is \({{\vec{r}}_{cm}}=\left( -0.42\hat{i}+2.3\hat{j} \right)m\)
(c) Centre of Mass of Continuous bodies: For calculating center of mass of a continuous body, we first divide the body into suitably chosen infinitesimal elements. The choice is usually determined by the symmetry of body.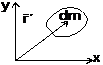
Consider element dm of the body having position vector , the quantity \({{m}_{i}}{{\vec{r}}_{i}}\) in equation of CM is replaced by dm and the discrete sum over particles ∑ m₁r₁/ M, becomes integral over the body:
\({{\vec{r}}_{CM}}=\frac{1}{M}\int_{{}}^{{}}{\vec{r}dm}\)
In component form this equation can be written as XCM = 1/M ∫ xdm; YCM = 1/M ∫ ydm and ZCM = 1/M ∫ zdm
To evaluate the integral we must express the variable m in terms of spatial coordinates x, y, z or \(\vec{r}\).
Example 4: The density of a thin rod of length l varies with the distance x from one end as ρ = ρ0 x2/l2. Find the position of centre of mass of rod.
Solution: Xcm = [∫lₒ (dm) x / ∫lₒ (dm)] = [∫lₒ (s. dx) (ρ0 x2/l2) x / ∫lₒ (s. dx) (ρ0 x2/l2)]
Here, s = area of cross section of rod.
Therefore, Xcm = 3l/4