Any device removing heat from the cold place and adding it to a hotter place is called a “refrigerator”. It is essentially a heat engine running back-wards. In a heat engine, the working substance takes in heat from a body at a higher temperature, converts a part of it into mechanical work, and gives out the rest to a body at a lower temperature. In refrigerator, a working substance takes in heat from a body at a lower temperature, has a net amount of work done on it by an external agent, and gives out a larger amount heat to a hot body (fig. 4). Thus, it continually transfer heat from a cold to a hot body at the expense of mechanical energy supplied to it by an external agent. The working substance is called “refrigerant”.
The engine employing the Carnot cycle may be adopted as a refrigerator. Each step in the cycle is reversible, therefore it is possible to reverse the entire cycle.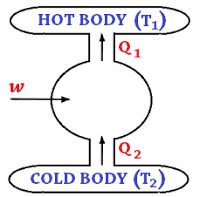 Let Q2 be the heat removed from the cold body at temperature T2, W the work done on the refrigerant, and Q1 the heat delivered to the hot body at temperature T1. Then, we have
Let Q2 be the heat removed from the cold body at temperature T2, W the work done on the refrigerant, and Q1 the heat delivered to the hot body at temperature T1. Then, we have
Q1 = Q2 + W
Or
W = Q1 – Q2 = Q2 (Q1/Q2 – 1)
As in Carnot’s, if we use an ideal gas as working substance, we can show that
Q1/Q2 = T1/T2
∴ W = Q2 (T1/T2– 1) = Q2 (T1– T2/T2)
This is the expression for the work that must be supplied to run the refrigerator.
Coefficient of Performance:
This purpose of the refrigerator is remove as much heat Q2as possible from the cold body with expenditure of a little work (W) as possible. Therefore, a measure of the performance of the refrigerator is expressed by the “coefficient of performance” K which is defined as the ratio of the heat taken from the cold body to the work needed to run the refrigerator. That is
K = Q2/W
Substituting the value of W in the above equation we get
K = T2/T1 – T2
This is the expression for the coefficient performance. A good refrigerator should have a high coefficient of performance, typically 5 or 6. Thicker and high quality insulation tends to increase the coefficient of performance.
Example: A refrigerator is to maintain eatables kept inside at 90C. If room temperature is 360C. Calculate the coefficient of performance.
Answer: Here T1 = 360C = 36 + 273 = 309K
T2 = 100C = 10 + 273 = 283K
COP = T2/T1 – T2 = 283/309 – 283
= 283/26 = 10.9
