Statement: When an incompressible and non-viscous liquid (or gas) flows in streamlined motion from one place to another, then at every point of its path the total energy per unit volume is constant.
That is \(\left( \frac{\text{Pressure energy}}{\text{Volume}}+\frac{\text{Kinetic energy}}{\text{Volume}}+\frac{\text{Potential energy}}{\text{Volume}} \right)\) = constant.
P + ½ ρv² + ρgh = constant
Thus, Bernoulli’s theorem is in one way the principle of conservation of energy for a flowing liquid (or gas).
Bernoulli’s Equation: Let us focus our attention on the motion of the shaded region. This is our “system”. The lower cylindrical element of fluid of length Δl₁ A₁ is at height y₁ which moves with speed v₁ After some time, the leading section of our system fills the upper cylinder of fluid of length Δl₂ and area A₂ at height y₂, and is then moving with speed v₂.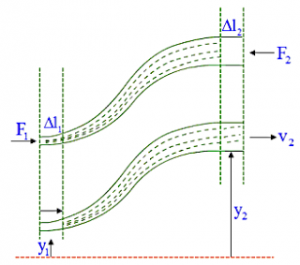
A pressure force F₁ acts on the lower part of the cylindrical tube towards right and pressure force F₂ acts on the upper part of the cylindrical tube towards left. The net work done on the system F₁ and F₂ is
W = F₁Δl₁ – F₂Δl₂ = P₁A₁Δl₁ – P₂A₂Δl₂ = (P₁ – P₂) ΔV
Where we have used the relations F = PA and ΔV = A₁Δl₁ – A₂Δl₂ the net effect of the motion of the system is to raise the height of the lower cylinder of mass and to change its speed. The changes in the potential and kinetic energies are
ΔU = Δmg (y₂ – y₁)
ΔK = ½ Δm (v₂² – v₁²)
W = ΔU + ΔK (P₁ – P₂) ΔV = Δmg (y₂ – y₁) + ½ Δm (v₂² – v₁²)
Since the density is ρ = Δm/ ΔV, we have P₁ + ρgy₁ + ½ ρv₁² = P₂ + ρgy₂ + ½ρv₂²
Since the points 1 and 2 can be chosen arbitrarily, we can express this result as Bernoulli’s Equation p + ρgy + ½ ρv² = constant
It is applied to all points along a streamline in a nonviscous, incompressible and irrotational fluid.
Example: Figure shows a liquid of density 1200 kg/m³ flowing steadily in a tube of varying cross-section. The cross-section at a point A is 1.0 cm² and that at B is 20 mm², the points A and B are in the same horizontal plane. The speed of the liquid at A is 10 cm/s. Calculate the difference in pressures at A and B.
Solution:
From equation of continuity, the speed V2 at B is given by,
A1V1 = A2V2
(1.0 cm²) (10 cm/s) = (20 mm²) v₂
\({{\nu }_{2}}=\frac{1.0\,c{{m}^{2}}}{20\,m{{m}^{2}}}\times 10\,cm/s=50\,cm/s\)
By Bernoulli’s equation,
P₁ + ρgh₁ + ½ ρv₁² = P₂ + ρgh₂ + ½ρv₂²
Here h1 = h2. Thus,
P₁ – P₂ = ½ρv₂² – ½ ρv₁² = ½ x (1200 kg/m³) (2500 cm²/s² – 100 cm²/ s²)
= 600 kg/ m³ x 2400 cm²/ s² = 144 Pa