Asymptotes of Hyperbola

Asymptotes of Hyperbola

If the length of the perpendicular from a point on a hyperbola to a straight line tends to zero as the point on the hyperbola moves to infinity along the hyperbola, then the straight line is called the asymptote of the hyperbola.

The asymptote of a hyperbola can be found as follows.

Let y = mx + c be the asymptote of the hyperbola \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=1\).

Solving these two equations, we get the quadratic as (b² – a²m²) x² – 2a² mcx – a² (b² + c²) = 0 … (i)

In order that y = mx + c be an asymptote, both roots of (i) must approach infinity, the conditions for which are as follows:

Coefficient of x² = 0

And coefficient of x = 0

Or b² – a²m² = 0

Or m = ± b/a and a²mc = 0

Or c = 0

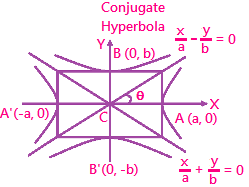
Therefore, the equations of the asymptotes are \(\frac{x}{a}+\frac{y}{b}=0\) and \(\frac{x}{a}-\frac{y}{b}=0\).

The combined equation of the asymptotes is \(\frac{{{x}^{2}}}{{{a}^{2}}}-\frac{{{y}^{2}}}{{{b}^{2}}}=0\).

Illustration 1:  Find the eccentricity of the hyperbola with asymptotes 3x + 4y = 2 and 4x – 3y = 2.

Solution:  Since the asymptotes are perpendicular, the hyperbola is rectangular and, hence, eccentricity is √2.

Illustration 2:  Find the equation of the hyperbola which has 3x – 4y + 7 = 0 and 4x + 3y + 1 = 0 as its asymptotes and which passes through the origin.

Solution:  The combined equation of the asymptotes is (3x – 4y + 7) (4x + 3y + 1) = 0

Or 12x² – 7xy – 12y² + 31x + 17y + 7 = 0 … (i)

Since, the equation of hyperbola and the combined equation of its asymptotes differ by a constant, the equation of the hyperbola may be taken as 12x² – 7xy – 12y² + 31x + 17y + k = 0 … (ii)

As (ii) passes through the origin (0, 0), we have k = 0.

Hence, the equation to the required hyperbola is 12x² – 7xy – 12y² + 31x + 17y = 0.