Area between a Curve and Axis

(i) The area bounded by the curve y = F(x) above the X-axis and between the lines x = a, y = b is given by ∫ₐ^b y dx = ∫ₐ^b F (x) dx.

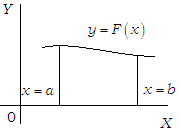
(ii) If the curve between the lines x = a, x = b lines below the X-axis, then the required area is given by |∫ₐ^b (-y) dx| = |-∫ₐ^by dx| = |-∫ₐ^b F(x) dx|.

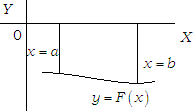
(iii) The area bounded by the curve x = F(y) right to the Y-axis and the lines y = c, y = d is given by ∫_c^d x dy =∫_c^d F (y) dy.

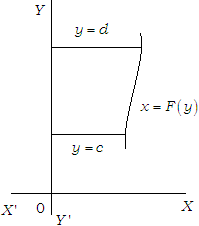
(iv) If the curve between the lines y = c, y = d left to the Y-axis, then the area is given by |∫_c^d (-x) dy = ∫_c^d x dy =∫_c^d F (y) dy|.

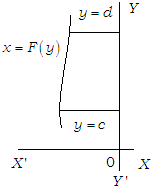
Whenever we solve this type of question. Generally, we follow the steps given below.

(i) First we sketch the given curve.

(ii) Now, we find the intersection of curve with axis and given line.

(iii) We select the bounded region in the figure and take interval between bounded region.

(iv) Now, we apply the appropriate formula to calculate the area of bounded region.

Example: The area of the region bounded by x² = 4y, y = 2, y = 4 and the Y-axis in the first quadrant is

Solution: To determine the required area, integrate x. with respect y and take y = 2 as lower limit and y = 4 as upper limit. The given curve x² = 4y is a parabola, which is symmetrical about Y-axis.

(Q it contains even power of x) only and passes through the region.

The area of the region bounded by the curve x² – 4y, y = 2.

And y = 4 and the Y-axis is shown in fig.

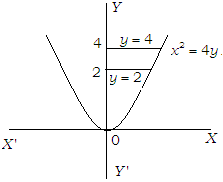
Required area (shaded region) = ∫^{y = b}_{y = a} |x|dy.

(Here |x| = √4y and a = 2, b = 4)

= ∫₂⁴ |x|dy (Q x² = 4y (∴ |x| = 2√y)

= 2[(y^3/2)/(3/2)]⁴₂ = 4/3 [4^3/2 – 2^3/2] = 4/3 [8 – 2√2] = 8/3 [4 – √2] sq units.

Area between the given curves: Area between two curves y = f(x), y = g(x) and the lines x = a and x = b is always given by ∫^bₐ (f(x) – g(x)) dx provided f(x) > g(x) in [a, b], the position of the graph is immaterial, as shown the steps given below.

(i) First we sketch the given curves. (if necessary)

(ii) Now we find the intersection points of the given curves by solving them.

(iii) Now we select the bounded region in the figure of curves and take the interval between bounded regions.

(iv) Now we apply the appropriate formula to calculate the area of bounded region.

Example: The area of the region bounded by the curves y = 2^x, y = 2x – x² and x = 2 is

Solution: Required area

= ∫₀² [2^x – (2x – x²)] dx

= ∫₀² [2^x – 2x + x²] dx

= [(2^x/log2) – x² + (x³/3)]₀²

= (4/log2) – 4 + 8/3 – 1/log2

= 3/log2 – 4/3 Sq Unit.