(i) Attraction between two closely parallel moving boats (or buses): When two boats or buses move side by side in the same direction, the water (or air) in the region between them moves faster than that on the remote sides. Consequently in accordance with Bernoulli’s principle the pressure between them is reduced and hence due to pressure difference they are pulled towards each other creating the so called attraction.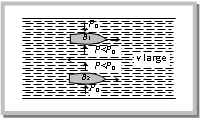 (ii) Working of an Aeroplane: This is also based on Bernoulli’s principle. The wings of the aeroplane are of the shape as shown in fig. Due to this specific shape of wings when the aeroplane runs, air passes at higher speed over it as compared to its lower surface. This difference of air speeds above and below the wings, in accordance with Bernoulli’s principle, creates a pressure difference, due to which an upward force called ‘dynamic lift’ (= pressure difference × area of wing) acts on the plane. If this force becomes greater than the weight of the plane, the plane will rise up.
(ii) Working of an Aeroplane: This is also based on Bernoulli’s principle. The wings of the aeroplane are of the shape as shown in fig. Due to this specific shape of wings when the aeroplane runs, air passes at higher speed over it as compared to its lower surface. This difference of air speeds above and below the wings, in accordance with Bernoulli’s principle, creates a pressure difference, due to which an upward force called ‘dynamic lift’ (= pressure difference × area of wing) acts on the plane. If this force becomes greater than the weight of the plane, the plane will rise up.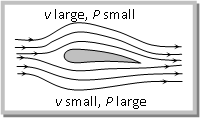 (iii) Action of atomiser: The action of carburetor, paint-gun, scent-spray or insect-sprayer is based on Bernoulli’s principle. In all these, by means of motion of a piston P in a cylinder C, high speed air is passed over a tube T dipped in liquid L to be sprayed. High speed air creates low pressure over the tube due to which liquid (paint, scent, insecticide or petrol) rises in it and is then blown off in very small droplets with expelled air.
(iii) Action of atomiser: The action of carburetor, paint-gun, scent-spray or insect-sprayer is based on Bernoulli’s principle. In all these, by means of motion of a piston P in a cylinder C, high speed air is passed over a tube T dipped in liquid L to be sprayed. High speed air creates low pressure over the tube due to which liquid (paint, scent, insecticide or petrol) rises in it and is then blown off in very small droplets with expelled air.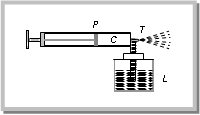 (iv) Blowing off roofs by wind storms: During a tornado or hurricane, when a high speed wind blows over a straw or tin roof, it creates a low pressure (P) in accordance with Bernoulli’s principle.
(iv) Blowing off roofs by wind storms: During a tornado or hurricane, when a high speed wind blows over a straw or tin roof, it creates a low pressure (P) in accordance with Bernoulli’s principle.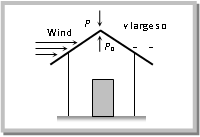 However, the pressure below the roof (i.e., inside the room) is still atmospheric (= Pₒ). So due to this difference of pressure the roof is lifted up and is then blown off by the wind.
However, the pressure below the roof (i.e., inside the room) is still atmospheric (= Pₒ). So due to this difference of pressure the roof is lifted up and is then blown off by the wind.
(v) Magnus effect: When a spinning ball is thrown, it deviates from its usual path in flight. This effect is called Magnus effect and plays as important role in tennis, cricket and soccer, etc. as by applying appropriate spin the moving ball can be made to curve in any desired direction.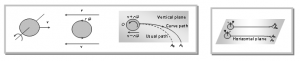 If a ball is moving from left to right and also spinning about a horizontal axis perpendicular to the direction of motion as shown in fig. then relative to the ball, air will be moving from right to left.
If a ball is moving from left to right and also spinning about a horizontal axis perpendicular to the direction of motion as shown in fig. then relative to the ball, air will be moving from right to left.
The resultant velocity of air above the ball will be (v + rω) while below it(v – rω). So in accordance with Bernoulli’s principle pressure above the ball will be less than below it. Due to this difference of pressure an upward force will act on the ball and hence the ball will deviate from its usual path OAₒ and will hit the ground at A₁ following the path OA₁ i.e., if a ball is thrown with back-spin, the pitch will curve less sharply prolonging the flight.
Similarly if the spin is clockwise i.e., the ball is thrown with top-spin, the force due to pressure difference will act in the direction of gravity and so the pitch will curve more sharply shortening the flight.
Furthermore, if the ball is spinning about a vertical axis, the curving will be sideways as shown in producing the so called out swing or in swing.
(vi) Venturimeter: It is a device based on Bernoulli’s theorem used for measuring the rate of flow of liquid through pipes.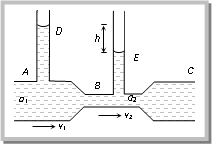 It consists of two identical coaxial tubes A and C connected by a narrow co-axial tube B. Two vertical tubes D and E are mounted on the tubes A and B to measure the pressure of the following liquid.
It consists of two identical coaxial tubes A and C connected by a narrow co-axial tube B. Two vertical tubes D and E are mounted on the tubes A and B to measure the pressure of the following liquid.
When the liquid flows in the tube ABC, the velocity of flow in part B will be larger than in the tube A or C. So the pressure in part B will be less than that in tube A or C. By measuring the pressure difference between A and B, the rate of flow of the liquid in the tube can be calculated.
Let a₁, a₂ = area of cross section of tube A and B respectively v₁, v₂ = Velocity of flow of liquid through A and B respectively
P₁, P₂ = Liquid pressure at A and B respectively
∴ P₁ – P₂ = hρg … (i) [ρ = density of flowing liquid]
From Bernoulli’s theorem for horizontal flow of liquid
P₁ + ½ ρv₁² = P₂ + ½ ρv₂²
P₁ – P₂ = ½ ρ (v₂² – v₁²) … (ii)
From (i) and (ii) hρg = ½ ρ (v₂² – v₁²) = \(\frac{1}{2}\rho \left[ \frac{{{V}^{2}}}{a_{2}^{2}}-\frac{{{V}^{2}}}{a_{1}^{2}} \right]\) [As V = a₁v₁ = a₂v₂]
∴ \({{V}^{2}}=\frac{2a_{1}^{2}a_{2}^{2}hg}{a_{1}^{2}-a_{2}^{2}}\) Or \(V={{a}_{1}}{{a}_{2}}\sqrt{\frac{2hg}{a_{1}^{2}-a_{2}^{2}}}\)
