Application of derivatives – Normal
Normal: The normal to the curve at any point P on it is the straight line which passes through P and is perpendicular to the tangent to the curve at P.
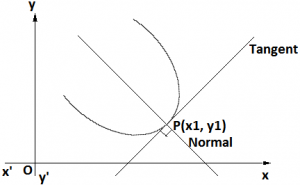
Slope of Normal: We know that normal to the curve at P (x₁, y₁) is a line perpendicular to tangent at P (x₁, y₁) and passing through P.
∴ Slope of the tangent at P = 1/ Slope of the tangent at P
⇒ Slope of normal at P (x₁, y₁) = \(-\frac{1}{{{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},\,{{y}_{1}} \right)}}}\),
⇒ Slope of normal at P (x₁, y₁) = \(-{{\left( \frac{dx}{dy} \right)}_{\left( {{x}_{1}},\,{{y}_{1}} \right)}}\).
Note: If normal is parallel to x – axis
⇒ \(-{{\left( \frac{dx}{dy} \right)}_{\left( {{x}_{1}},\,{{y}_{1}} \right)}}\,=\,0\) or \({{\left( \frac{dx}{dy} \right)}_{\left( {{x}_{1}},\,{{y}_{1}} \right)}}\,=\,0\),
If normal is perpendicular to x – axis (perpendicular to y – axis).
⇒ \(-{{\left( \frac{dy}{dx} \right)}_{\left( {{x}_{1}},\,{{y}_{1}} \right)}}\,=\,0\).
Example: The slope of the normal to the curve x = 1- sin θ, y = b cos θ at θ = π/2 is
Solution: Given that,
x = 1- sin θ,
y = b cos θ
at θ = π/2
differentiation x and y w. r. t ‘θ’
dx/dθ = 0 – cos θ.
dx/dθ = – cos θ
dy/dθ = – b sinθ
\(\frac{\frac{dy}{d\theta }}{\frac{dx}{d\theta }}=\frac{-b\sin \theta }{-\cos \theta }=\frac{b\sin \theta }{\cos \theta }\),
dy/dx = b sinθ/ cosθ
we know that
⇒ Slope of normal at θ = \(-\frac{1}{\left( \frac{dy}{dx} \right)}\),
Where θ = π/2
Slope of tangent dy/dx = b/0
Slope of tangent = 0.
