⇒ Generally matter expands on heating and contracts on cooling. In case of water, it expands on heating if its temperature is greater than 4°C. In the range 0°C to 4°C, water contracts on heating and expands on cooling, i.e. g is negative. This behaviour of water in the range from 0°C to 4°C is called anomalous expansion.
⇒ The anomalous behavior of water arises due to the fact that water has three types of molecules, viz., H2O, (H2O)2 and (H2O)3 having different volume per unit mass and at different temperatures their properties in water are different.
⇒ At 4°C, density of water is maximum while its specific volume is minimum.
During winter when the water at the surface of a lake cools below 4°C by cool air, it expands and becomes lighter than water below. Therefore the water cooled below 4°C stays on the surface and freezes when the temperature of surroundings falls below 0°C. Thus the lake freezes first at the surface and water in contact with ice has temperature 0°C while at the bottom of the lake 4°C [as density of water at 4°C is maximum] and fish and other aquatic animals remain alive in this water.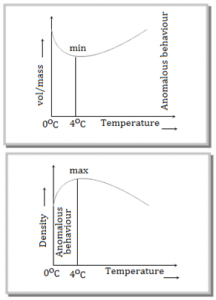
When matter is heated without any change in state, it usually expands. According to atomic theory of matter, a symmetry in potential energy curve is responsible for thermal expansion. As with rise in temperature the amplitude of vibration and hence energy of atoms increases, hence the average distance between the atoms increases. So the matter as a whole expands.
⇒ Thermal expansion is minimum in case of solids but maximum in case of gases because intermolecular force is maximum in solids but minimum in gases.
⇒ Solids can expand in one dimension (linear expansion), two dimension (superficial expansion) and three dimension (volume expansion) while liquids and gases usually suffers change in volume only.
⇒ The coefficient of linear expansion of the material of a solid is defined as the increase in its length per unit length per unit rise in its temperature.
α = ΔL/L x 1/ΔT
Similarly the coefficient of superficial expansion β = ΔA/A x 1/ΔT
And coefficient of volume expansion γ = ΔV/V x 1/ΔT
The value ofa, b and g depends upon the nature of material. All have dimension [θ¯¹] and unit per °C.
⇒ As α = ΔL/L x 1/ΔT, β = ΔA/A x 1/ΔT and γ = ΔV/V x 1/ΔT
∴ ΔL = Lα ΔT, ΔA = Aβ ΔT and ΔV = Vγ ΔT
Final length L’ = L + ΔL = L (1 + αΔT) …..(i)
Final area A’ = A + ΔA = A (1 + βΔT) …..(ii)
Final volume V’ = V + ΔV = V (1 + ɣΔT) …..(iii)
⇒ If L is the side of square plate and it is heated by temperature DT, then its side becomes L’.
The initial surface area A = L2 and final surface A’ = L’2
∴ \(\frac{{{A}’}}{A}={{\left( \frac{{{L}’}}{L} \right)}^{2}}={{\left( \frac{L(1+\alpha \Delta T)}{L} \right)}^{2}}\) = (1 + αΔT)² = (1 + 2αΔT) [Using Binomial theorem]
Or A’ = A (1 + 2αΔT)
Comparing with equation (ii) we get b = 2a
Similarly for volumetric expansion \(\frac{{{V}’}}{V}={{\left( \frac{{{L}’}}{L} \right)}^{3}}={{\left( \frac{L(1+\alpha \,\Delta T)}{L} \right)}^{3}}\)= (1 + αΔT)³ = (1 + 3αΔT) [Using Binomial theorem].
Or V’ = V (1 + ɣΔT)
Comparing with equation (iii), we get ɣ = 3α
So α : β : ɣ = 1 : 2 : 3
(i) Hence for the same rise in temperature
Percentage change in area = 2 ´ percentage change in length.
Percentage change in volume = 3 ´ percentage change in length.
(ii) The three coefficients of expansion are not constant for a given solid. Their values depends on the temperature range in which they are measured.
(iii) The values of a, b, g are independent of the units of length, area and volume respectively.
(1) Bi-metallic strip: Two strips of equal lengths but of different materials (different coefficient of linear expansion) when join together, it is called “bi-metallic strip”, and can be used in thermostat to break or make electrical contact. This strip has the characteristic property of bending on heating due to unequal linear expansion of the two metal. The strip will bend with metal of greater a on outer side i.e. convex side.
(2) Effect of temperature on the time period of a simple pendulum: A pendulum clock keeps proper time at temperatureq. If temperature is increased to θ’ (> θ) then due to linear expansion, length of pendulum and hence its time period will increase.
Time period \(T=2\pi \sqrt{\frac{L}{g}}\Rightarrow \frac{{{T}’}}{T}=\sqrt{\frac{{{L}’}}{L}}=\sqrt{\frac{L(1+\alpha \,\Delta \theta )}{L}}=\sqrt{(1+\alpha \,\Delta \theta )}\)
T’ = T (1 + ½ αΔθ) = ½ α ΔθT or (T’ – T)/T = ½ α Δθ
∴ ΔT/T = ½ α Δθ
(i) Due to increment in its time period, a pendulum clock becomes slow in summer and will lose time.
Loss of time in a time period ΔT = ½ α ΔθT
∴ Loss of time in any given time interval t can be given by Δt = ½ α Δθt.
(ii) The clock will lose time i.e. will become slow if θ’ > θ (in summer) and will gain time i.e. will become fast if θ’ < θ (in winter).
(iii) The gain or loss in time is independent of time period T and depends on the time interval t.
(iv) Time lost by the clock in a day (t = 86400 sec)
Δt = ½ α Δθ t = ½ α Δθ (86400) = 43200 α Δθ sec.
(v) Since coefficient of linear expansion (a) is very small for invar, hence pendulums are made of invar to show the correct time in all seasons.
(3) Expansion of cavity: Thermal expansion of an isotropic object may be imagined as a photographic enlargement. So if there is a hole A in a plate C (or cavity A inside a body C), the area of hole (or volume of cavity) will increase when body expands on heating, just as if the hole (or cavity) were solid B of the same material. Also the expansion of area (or volume) of the body C will be independent of shape and size of hole (or cavity), i.e., will be equal to that of D.
Latent Heat:
(1) When a substance changes from one state to another state (say from solid to liquid or liquid to gas or from liquid to solid or gas to liquid) then energy is either absorbed or liberated. This heat energy is called latent heat.
(2) No change in temperature is involved when the substance changes its state. That is, phase transformation is an isothermal change. Ice at 0°C melts into water at 0°C. Water at 100°C boils to form steam at 100°C.
(3) The amount of heat required to change the state of the mass m of the substance is written as: DQ = mL, where L is the latent heat. Latent heat is also called as Heat of Transformation.
(4) Unit: cal/gm or J/kg and Dimension: [L2T-2]
(5) Any material has two types of latent heats
(i) Latent heat of fusion: The latent heat of fusion is the heat energy required to change 1 kg of the material in its solid state at its melting point to 1 kg of the material in its liquid state. It is also the amount of heat energy released when at melting point 1 kg of liquid changes to 1 kg of solid. For water at its normal freezing temperature or melting point (0°C), the latent heat of fusion (or latent heat of ice) is
LF = Lice ≈ 80 cal/g ≈ 60 kj/mol ≈ 336 kilo joule / kg.
(ii) Latent heat of vaporization: The latent heat of vaporization is the heat energy required to change 1 kg of the material in its liquid state at its boiling point to 1 kg of the material in its gaseous state. It is also the amount of heat energy released when 1 kg of vapour changes into 1 kg of liquid. For water at its normal boiling point or condensation temperature (100°C), the latent heat of vaporization (latent heat of steam) is
Lv = Lsteam ≈ 540 cal/g ≈ 40.8 kj/mol≈2260 kilo joule/kg
Scales of Temperature: The Kelvin temperature scale is also known as thermodynamic scale. The S.I. unit of temperature is kelvin and is defined as (1/273.16) of the temperature of the triple point of water. The triple point of water is that point on a P-T diagram where the three phases of water, the solid, the liquid and the gas, can coexist in equilibrium.
In addition to kelvin temperature scale, there are other temperature scales also like Celsius, Fahrenheit, Reaumer, Rankine etc.
To construct a scale of temperature, two fixed points are taken. First fixed point is the freezing point of water, it is called lower fixed point. The second fixed point is the boiling point of water, it is called upper fixed point.
Temperature on one scale can be converted into other scale by using the following identity.
\(\frac{\text{Reading on any scale}-\text{Lower fixed point (LFP)}}{\text{Upper fixed point (UFP)}-\text{ Lower fixed point (LFP)}}=\text{Constant for all scales}\).
\(\frac{C-0}{100}=\frac{F-32}{212-32}=\frac{K-273.15}{373.15-273.15}\).
Or \(\frac{C}{5}=\frac{F-32}{9}=\frac{K-273}{5}\).
Where “C” is temperature in Celsius scale, “F” is in Fahrenheit scale and “K” is in Kelvin scale.