Angle of intersection of Two Circles: The angle of intersection of two circles is defined as the angle between the tangents to the two circles at their point of intersection.
Let,
x² + y² + 2g₁x + 2f₁y + c₁ = 0
x² + y² + 2g₂x + 2f₂y + c₂ = 0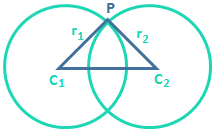
\(\cos \left( \angle {{C}_{1}}P{{C}_{2}} \right)=\frac{{{C}_{1}}{{P}^{2}}+{{C}_{2}}{{P}^{2}}-{{C}_{1}}{{C}_{2}}}{2{{C}_{1}}P.{{C}_{2}}P}\).
\(\cos P=\frac{r_{1}^{2}+r_{2}^{2}-{{d}^{2}}}{2{{r}_{1}}{{r}_{2}}}\).
Orthogonal Circles: Two circles are said to be intersect orthogonally, if their angle of intersection is right angle.
cos (∟C₁PC₂) = 0.
C₁P² + C₂P² – C₁C₂² = 0.
g₁² + f₁² – c₁ + g₂² + f₂² – c₂ = g₁² – 2g₁g₂ + 2f₁f₂ + f₂² + f₁² + g₂².
2 (g₁ g₂ + f₁ f₂) = c₁ + c₂.
This is the condition for orthogonality of circles.