Adsorption isotherms: Plot of the amount of gas adsorbed on the surface of the adsorbent and pressure at constant temperature.
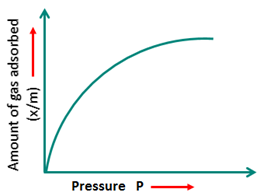1. Freundlich adsorption isotherm:
\(\frac{x}{m}=k.{{P}^{\frac{1}{n}}}\) (n > 1) … 1
x = mass of the gas adsorbed
m = mass of the adsorbent
P = pressure
k, n = constants. Depend on the nature of the adsorbent and the gas
Taking logarithm of eqn 1 →\(\log \left( \frac{x}{m} \right)=\log k+\frac{1}{n}\log P\)
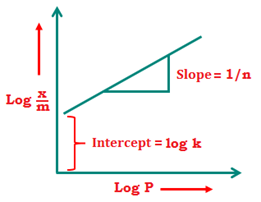
The plot of log(x/m) and log P is a straight line. If the plot is not a straight line then Freundlich isotherm is not valid. The slope of the straight line is 1/n and the y intercept is equal to k.
If 1/n = 0, then x/m is constant and doesn’t depend on pressure
If 1/n = 1, then x/m α P
2. Langmuir adsorption isotherm:
Postulates:
⇒ Gases undergoing adsorption behave ideally
⇒ The surface containing the adsorbing sites is perfectly flat plane with no corrugations (assume the surface is homogeneous).
⇒ The adsorbing gas adsorbs into an immobile state.
⇒ All sites are equivalent.
⇒ Each site can hold at most one molecule of gas (mono-layer coverage only).
⇒ There are no interactions between adsorbate molecules on adjacent sites.
⇒ Dynamic equilibrium exists between adsorbed gaseous molecules and the free gaseous molecules
Where A(g) is unabsorbed gaseous molecule, B(s) is unoccupied metal surface and AB is Adsorbed gaseous molecule. He gave the following relation:
x\(\frac{P}{x/m}=\frac{1}{{{K}’}}+\left( \frac{K}{{{K}’}} \right)P\Rightarrow \frac{x}{m}=\frac{{K}’P}{1+KP}\)
\(K=\frac{{{k}_{ad}}}{{{k}_{d}}}\), kad = adsorption rate constant, kd = description rate constant
K’ = kK
The plot of x\(\frac{P}{x/m}\) and P is a straight line, whose slope is (K/K’) and y intercept is (1/K’)
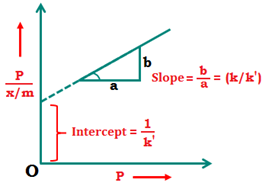
When pressure is very high, then 1 + KP = KP
Thus, at high pressures the degree of adsorption approaches a limiting value.
When pressure is low then 1 + KP = 1
\(\frac{x}{m}={K}’P\)
The degree of adsorption is directly proportional to pressure
Adsorption from solution phase:
⇒ The adsorption decreases with increase in temperature.
⇒ Adsorption increases with increase in surface area.
⇒ The extent of adsorption depends on concentration of solute in solution.
⇒ The extent of adsorption depends on nature of adsorbent and adsorb ate.
The Freundlich equation is modified as \(\frac{x}{m}=k.{{C}^{\frac{1}{n}}}\)
C – Equilibrium concentration
\(\log \left( \frac{x}{m} \right)=\log k+\frac{1}{n}\log C\)
Positive adsorption: The concentration of adsorbate is more on the surface of adsorbent than in the bulk of the solution
Negative adsorption: The concentration of adsorbate is more in the bulk of the solution than in the surface of the adsorbent.