Acceleration – Time Graph of Various Types of Motions of a Particle

Acceleration – Time Graph of Various Types of Motions of a Particle

Let the acceleration be given as the function of time, i.e. a = f (t). Then the elementary change in velocity during a time dt is \(d\overrightarrow{v}=\overrightarrow{a}dt\). We can observe that in a – t graph, \(\overrightarrow{a}dt\) is equal to the area of the shaded elementary strip.

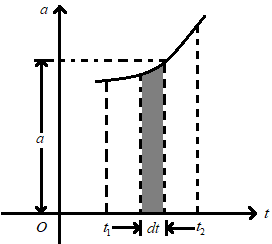
Summing up all the elementary areas dA, we have the total area \(A=\int{dA=\int{\overrightarrow{a}\,}}dt\). Since, \(\int\limits_{{{t}_{1}}}^{{{t}_{2}}}{\overrightarrow{a}\,dt}=\int\limits_{{{v}_{1}}}^{{{v}_{2}}}{\overrightarrow{dv}}=\Delta \overrightarrow{v}\); We have \(\Delta \overrightarrow{V}=\int{\overrightarrow{a}}\,dt\) = A = Area under a – t graph. That means, the change in velocity \(\Delta \overrightarrow{v}\) over any time interval is represented by the algebraic sum of all positive and negative area which we call area under a – t graph over that time interval, \(A=\sum{{{A}_{+}}}+\sum{{{A}_{-}}}\). If the area is negative, \(\Delta \overrightarrow{v}\) is negative, \(\Delta \overrightarrow{v}\) is directly in negative direction of coordinate axes. When area is zero, \(\Delta \overrightarrow{v}=0\), which means no change in velocity.

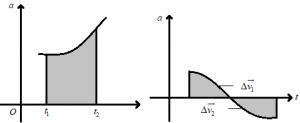
\(\Delta \overrightarrow{V}=\int{\overrightarrow{a}}\,dt\) = Area under v – t graph; \({{A}_{+}}\to \Delta \overrightarrow{{{v}_{1}}}\) is + ve; \({{A}_{-}}\to \Delta \overrightarrow{{{v}_{2}}}\) is – ve.

When \(\Delta \overrightarrow{V}\) is positive, you should not immediately accept it as \(\Delta |\overrightarrow{V}|>0\), because \(\Delta \overrightarrow{V}\) is a vector quantity. Hence, positive area means a positive \(\Delta \overrightarrow{v}\) but not positive \(\Delta \overrightarrow{v}\,(\ne \Delta V)\).