AC Voltage applied to a Capacitor

When a capacitor is connected to a voltage source in a dc circuit, current will flow for the short time required to charge the capacitor. As charge accumulates on the capacitor plates, the voltage across them increases, opposing the current. That is a capacitor in a dc circuit will limit or oppose the current as it charges. When the capacitor is fully charged, the current in the circuit falls to zero.

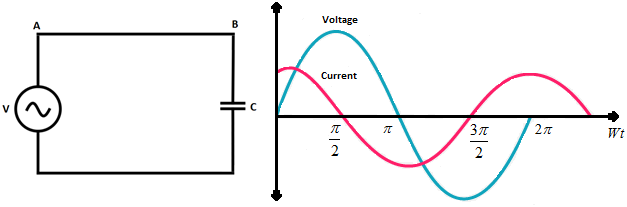
When the capacitor is connected to an AC source, it limits or regulates the current, but does not completely prevent the flow of charge. The capacitor is alternately charged and discharged as the current reverse each half cycle.

Let, q be the charge on the capacitor at any time t. the instantaneous voltage v across the capacitor is V = q/ C.

From the Kirchhoff’s loop rule, the voltage across the source and the capacitor are equal:

\({{v}_{m}}\sin \omega t=\frac{q}{C}\).

To find the current, we use the relation: \(i=\frac{dq}{dt}\).

\(i=\frac{d}{dt}\left( {{v}_{m}}C\sin \omega t \right)=\omega C{{v}_{m}}\cos \left( \omega t \right)\).

Using the relation: \(\cos (\omega t)=\sin \left( \omega t+\frac{\pi }{2} \right)\).

\(i={{i}_{m}}\sin \left( \omega t+\frac{\pi }{2} \right)\).

Where the amplitude of the oscillating current is i_m = ωCv_m. We can rewrite it as:

\({{i}_{m}}=\frac{{{v}_{m}}}{\left( 1/\omega C \right)}\).

Comparing it to \({{i}_{m}}=\frac{v}{R}\) for a purely resistive circuit, we find that (1/ ωC) plays the role of resistance. It is called capacitive reactance and is denoted by X_c.

\({{X}_{C}}=\frac{1}{\omega C}\).

So that the amplitude of the current is:

\({{i}_{m}}=\frac{{{v}_{m}}}{{{X}_{C}}}\).

In the above equations, the dimension of the capacitive resistance can be seen to be the same as that of resistance and also, the SI unit of capacitance is given as Ohm. The capacitive resistance restricts the passage of current in a purely capacitive circuit the same way as resistance hinders the passage of current in a purely resistive circuit.

Here we say, that the capacitive resistance is inversely proportional to the frequency and the capacitance. We also see from the above equations that the current in a capacitive circuit is π/2 ahead of the voltage across the capacitor.

The instantaneous power supplied to the capacitor can be given in terms of the current passing through the capacitor as:

P_C = iv = i_m cosωt v_m sinωt

\({{P}_{C}}=\frac{{{i}_{m}}{{v}_{m}}}{2}\sin 2\omega t\).

Here, the average power supplied over a complete cycle can be:

\({{P}_{C}}=\frac{{{i}_{m}}{{v}_{m}}}{2}\sin 2\omega t=0\).

So, we can say that in the case of a capacitor the current leads the voltage by π/2.