Sir Isaac Newton gave a mathematical relation to calculate the force of gravitation and this relation is known as the universal law of gravitation.
It is a common belief that an apple fell on Newton’s head and he realized that gravity exists. This isn’t completely incorrect. But Newton already knew about the existence of gravity. He was just trying to find out if the gravitational pull of the earth was what was holding the moon in its orbit
He knew that the earth exerted a gravitational force on objects on earth, he just wanted to know if it extended far enough to influence the moon as well. Based on the falling apple, he already knew that the force exerted between bodies is dependent on the masses and that they influence each other. Now he had to figure how the distance comes into play.
What is Universal Law of Gravitation?
According to this law “Every particle in the universe attracts every other particle with a force which is directly proportional to the product of their masses and inversely proportional to the square of the distance between them, the direction of the force being along the line joining the masses”.
Consider two objects of masses m1 and m2 separated by a distance d. According to the law of gravitation, the force of gravitation F is proportional to the product of the masses, F α m₁m₂ … (1)
And inversely proportional to the square of the distance between the masses, \(F\,\alpha \,\frac{1}{{{d}^{2}}}\) … (2)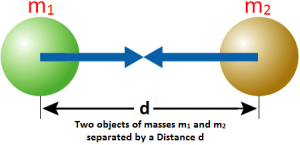
Combining equation (1) and equation (2), we get
\(F\,\alpha \,\frac{{{m}_{1}}{{m}_{2}}}{{{d}^{2}}}\),
\(F\,\alpha \,\frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{2}}}\) … (3)
Where G is a constant of proportionality called the universal gravitational constant. G is called universal constant because its value remains the same throughout the universe and is independent of masses of the objects.
Universal Gravitational Constant: The mathematical form of Newton’s Law of Gravitation is, \(F\,\alpha \,\frac{G{{m}_{1}}{{m}_{2}}}{{{d}^{2}}}\)
If m₁ = m₂ = 1, d = 1, then \(F\,=\,\frac{G\times 1\times 1}{{{1}^{2}}}\)
F = G
Hence universal gravitational constant may be defined as the force of gravitation existing between two unit masses separated by unit distance.
SI unit of gravitational constant \(G\,=\,\frac{F{{d}^{2}}}{{{m}_{1}}{{m}_{2}}}\)
SI unit of force F is N, SI unit of distance is metres and that of mass is kg.
SI Unit of \(G\,=\,\frac{N{{m}^{2}}}{kg\times kg}\)
SI unit of G = Nm²/kg² or Nm² kg¯¹
The experimental value of G = 6.6734 x 10¹¹ Nm²/kg².